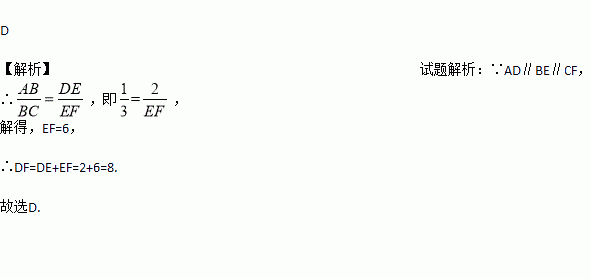��Ŀ����
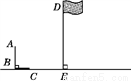
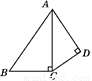
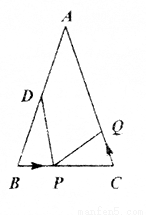
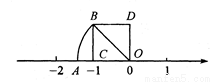
��ͼ��AD��BE��CF��ֱ��l1��l2������ƽ���߷ֱ��ڵ�A��B��C�͵�D��E��F����֪AB=1��BC=3��DE=2����DF�ij�Ϊ�� ��
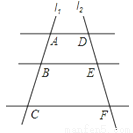
A. 4 B. 5 C. 6 D. 8
D �������������������AD��BE��CF�� �࣬���� ��ã�EF=6�� ��DF=DE+EF=2+6=8. ��ѡD.��ɽ����2015��ˮ������Ϊ100�֣�2017��ˮ������Ϊ144�֣���ù�ˮ����������ƽ��������.��ù�ˮ����������ƽ��������Ϊ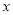 �������������з���Ϊ�� ��
�������������з���Ϊ�� ��
A.  B.
B. 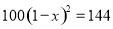
C. 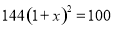 D.
D. 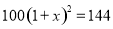
Ҫ��Сǿ��С����С�����������ѡ������Ϊ���֣���Сǿ��С��ͬʱ��ѡ�ĸ�����( )
A. 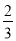 B.
B. 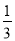 C.
C. 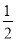 D.
D. 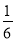
������������ʹƽ���ı���ABCDΪ���ε���( )
��AC��BD���ڡ�BAD��90�㣻��AB��BC����AC��BD.
A. �٢� B. �ڢ� C. �ۢ� D. �٢ڢ�
�鿴����ͼ�������������ͼ��(����)
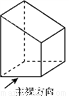

A. ��A�� B. ��B�� C. ��C�� D. ��D��
�鿴��һԪ���η���x(x��3)��4�Ľ���( )
A. 1 B. 4 C. ��1��4 D. 1��4
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���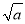 ��ƽ��������
��ƽ��������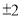 ����ô
����ô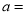 ______.
______.
9��ƽ������_______
�鿴����֪����ͼ��һ�ִ���16����/ʱ���ٶȴӸۿ�A�����������У���һ�ִ���12����/ʱ���ٶ�ͬʱ�Ӹۿ�A�������Ϸ����У��뿪�ۿ�2Сʱ��,���������( )
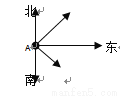
A��25���� B��30���� C��35���� D��40����
�鿴����ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1�� 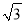 �������C������Ϊ�� ��
�������C�������� ��
A. ���� ��1�� B. ����1��
��1�� B. ����1��  �� C. ��
�� C. ��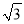 ��1�� D. ����
��1�� D. ����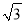 ����1��
����1��
��Rt��ABC�У���C��90�㣬��A, ��B, ��C���Եı߷ֱ�Ϊa��b��c, ��֪a��b��3��4��c��10�����ABC�����Ϊ( )
A. 24 B. 12 C. 28 D. 30
�鿴��.��ͼ���ȱߡ�ABC�߳�Ϊ3cm������ABC��AC����ƽ��1cm���õ���DEF�����ı���ABEF���ܳ�( )
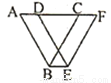
A. 9cm B. 10cm C. 11cm D. 12cm
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ��Rt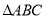 �У�
�У� 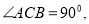 CD��б��AB�ĸ�.
CD��б��AB�ĸ�.
��֤�� 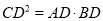 .
.
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ���ABC�Ķ�����ڸ���ϣ�����ƽ��ֱ������ϵ��A������Ϊ��-4,1������B������Ϊ��-2,1��.
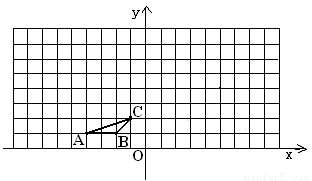
��1��������ABC��C��˳ʱ����ת90���õ��ġ�A1B1C1��д��A1������ꣻ
��2����ԭ��OΪλ�����ģ�λ�Ʊ�Ϊ2���ڵڶ�����������ABC��λ��ͼ�Ρ�A2B2C2,��д��C2������.
�鿴����ͼ�����꼶(1)���С����С����λͬѧȥ�ٳ��������DE�ĸ߶ȣ���ֱ֪���ڵ����ϵ����AB�ij�Ϊ3 m��ijһʱ�̣�������AB�������µ�ͶӰBC�ij�Ϊ2 m��
(1)������ͼ�л�����ʱ���DE�������µ�ͶӰ����д����ͼ���裻
(2)�ڲ������AB��Ӱ��ʱ��ͬʱ������DE�������µ�Ӱ��Ϊ6 m������������DE�ĸ߶ȣ�
�ⷽ�̣�x��5��x2��25.
�鿴����ͼ���ڡ�ABC�У�AD��BE�Ǹߣ���ABE=45�㣬��F��AB���е㣬AD��FE��BE�ֱ��ڵ�G��H����CBE=��BAD�������н��ۣ���FD=FE����AH=2CD����BC•AD=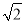 AE2����S��ABC=4S��ADF��������ȷ����___________��
AE2����S��ABC=4S��ADF��������ȷ����___________��
��ͼ��������ֱ���������У���ACB����ADC��90�㣬AC�� ��AD��2.��AB��_______ʱ����ABC���ACD���ƣ�
��AD��2.��AB��_______ʱ����ABC���ACD���ƣ�
- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��m��n��һԪ���η���x2+2x��7=0������������m2+3m+n=__��
5 ��������������������ݸ���ϵ���Ĺ�ϵ��֪m+n=��2����֪m�Ƿ��̵ĸ������Կɵ�m2+2m��7=0�����ɽ�m2+3m+n���m2+2m+m+n�����տɵô𰸣� ����m��n��һԪ���η���x2+2x��7=0���������� ��m+n=��2�� ��m��ԭ���̵ĸ��� ��m2+2m��7=0����m2+2m=7�� ��m2+3m+n=m2+2m+m+n=7��2=5 ���㣺����ϵ���Ĺ�ϵ ...��ͼ����ƽ��ֱ������ϵ�У���֪��A��1��1����B����1��1����C����1����2����D��1����2������һ����Ϊ2017����λ������û�е��Ե�ϸ�ߣ��ߵĴ�ϸ���Բ��ƣ���һ�˹̶���A��������A��B��C��D��A���Ĺ��ɽ������ı���ABCD�ı��ϣ���ϸ�ߵ���һ������λ�õĵ�������ǣ�����
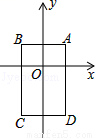
A. ��-1��-2�� B. ��-1��1�� C. ��-1��-1�� D. ��1��-2��
�鿴����ͼ����ƽ��ֱ������ϵ�У���֪��A��-3��6����B��-9��-3������ԭ��OΪλ�����ģ����Ʊ�Ϊ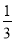 ���ѡ�ABO��С�����A�Ķ�Ӧ��A���������( )
���ѡ�ABO��С�����A�Ķ�Ӧ��A���������( )
A. ��-1��2�� B. ��-1��2����1��-2��
C. ��-9��18����9��-18�� D. ��1��-2��
�鿴����ABC���DEF�����Ʊ�Ϊ1��4�����ABC���DEF���ܳ���Ϊ���� ����
A. 1��2 B. 1��3 C. 1��4 D. 1��16
�鿴������x�ķ���x2+kx��1=0�ĸ�������ǣ�����
A. ����������ȵ�ʵ���� B. ��������ȵ�ʵ����
C. ֻ��һ��ʵ���� D. û��ʵ����
�鿴����ͼ��AD��BE��CF��ֱ��l1��l2������ƽ���߷ֱ��ڵ�A��B��C�͵�D��E��F����֪AB=1��BC=3��DE=2����DF�ij�Ϊ�� ��

A. 4 B. 5 C. 6 D. 8
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
һԪ���η���x(x��3)��4�Ľ���( )
A. 1 B. 4 C. ��1��4 D. 1��4
C �������������������x��x-3��=4�� ��x2-3x-4=0�� �ࣨx-4����x+1��=0�� ��x-4=0��x+1=0�� ��x1=4��x2=-1�� ��ѡC����֪����P�ǡ�MAN�Ľ�ƽ������һ�㣬PB��AM��B��PC��AN��C.
��1����ͼ1����D��E�ֱ����߶�AB��AC�ϣ��ҡ�DPE=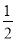 ��BPC����֤��DE=BD+CE��
��BPC����֤��DE=BD+CE��
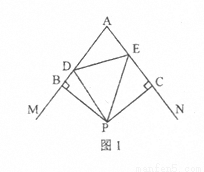
��2����ͼ2����D��AB���ӳ����ϣ�E��ֱ��AC�ϣ���DE��BD��CE���ߵ�������ϵ�仯�����仯����ֱ��д�����ۼ��ɡ�
�Ķ����в��ϣ�
��1���ⷽ�̣� 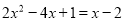
��������
���̻�Ϊ�� 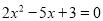 .
.
��������2x-3����x-1��=0��
�� 2x-3=0��x-1=0��
��ã�x=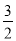 ��x=1.
��x=1.
��̵ĸ�Ϊ�� 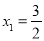 ��
�� 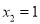 .
.
��2������ʽ���̵Ĺ����ǣ�����ʽ���̻�Ϊ��ʽ���̣�Ȼ�������ʽ���̣�Ȼ���������̵ĸ������������ȥ�������õ��ĸ�����ԭ���̵ĸ�.
�ο��������ϣ�����������⣺
��1���ⷽ�̣� 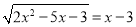 ��
��
��2��������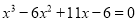 ��һ������x=1���̵���������__________.
��һ������x=1���̵���������__________.
��֪����ͼ��Rt��ABC�У���BAC=90��.
��1����Ҫ����ͼ����������ͼ�ۼ���
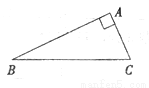
���ӳ�BC����D��ʹCD=BC��
���ӳ�CA����E��ʹAE=2CA��
������AD��BE�������߶�AD��BE�Ĵ�С��ϵ��
��2��֤����1��������߶�AD��BE��С��ϵ�IJ���.
��������
��1��AD��BE�Ĵ�С��ϵ��________________.
��2��֤����
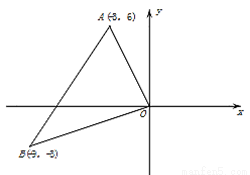
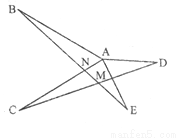
�鿴����֪����ͼ��AB=AC��AD=AE����BAC=��DAE=����BE��AC��CD�ֱ��ཻ�ڵ�N��M.
��1����֤��BE=CD��
��2�����BMC�Ĵ�С.���æ���ʾ��
2017��9��17�գ�����ı�������У����ȫ��ͬѧ����ѧУ30ǧ�ķ�ɽũҵְҵѧԺ���μ�Ϊ��һ�ܵ�ѧũ�Ͷ���ͬѧ�dz�����ͳ�ǰ��������ʦ��ѧУ������������5���ӣ���˽�ҳ�ǰ���������ͬѧ��ͬʱ������ũְԺ����֪����ʦ����˽�ҳ����ٶ��Ǵ�ͳ��ٶȵ�1.2�������ͳ�������ʦ����˽�ҳ����ٶȷֱ��Ƕ��٣�
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�Ȼ�������ֵ�� 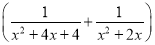 ��
��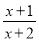 ������x=3.
������x=3.
�ⷽ�̣� 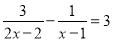
���㣺
��1��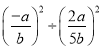 ��
��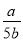
��2��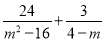
�ֽ���ʽ��
��1��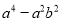
��2��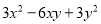
��ͼ���ڡ�ABC�У�AB=AC=24���ף���ABC=��ACB��BC=16���ף���DΪAB���е㣬�����P���߶�BC����4����/����ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶�������Q���˶��ٶ�Ϊ______����/��ʱ���ܹ���ijһʱ��ʹ��BPD���CQPȫ��.
��֪��ͼ��D�ǡ�ABC�������ƽ���ߵĽ��㣬����˵����
��AD=CD
��D����ABC����������ֱ�ߵľ������
�۵�D�ڡ�B��ƽ������
������B=80�㣬���D=50��
������ȷ��˵���������_____________________.
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����ʽ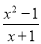 ��ֵΪ�㣬��x��ֵ�ǣ� ��
��ֵΪ�㣬��x��ֵ�ǣ� ��
A. 1 B. 0 C. -1 D. ��1
A ��������������-1=0���ҷ�ĸx+1��0����x=1ʱ����ʽ��ֵΪ�㣬��ѡA���и���ʽ�У���ȷ���ǣ� ��
A. 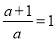 B.
B. 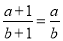
C. 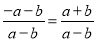 D.
D. 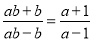
��ͼ����֪AB=AD����ô��������һ�������������ж���ABC�ա�ADC���ǣ�������
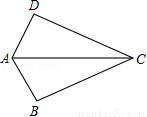
A. CB=CD B. ��BAC=��DAC C. ��BCA=��DCA D. ��B=��D=90��
�鿴�����и�ʽ����ߵ��ұߵı����У�����ʽ�ֽ���ǣ� ��
A��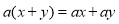
B��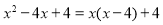
C��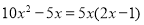
D��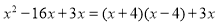
���и�ʽ�У���ʽ�ĸ���Ϊ �� ��
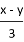 ��
��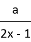 ��
��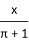 ��
��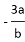 ��
��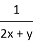 ��
��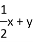 ��
��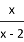 .
.
A. 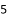 �� B.
�� B. 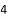 �� C.
�� C. 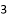 �� D.
�� D. 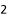 ��
��
�ڵ������ڣ����ɹ�������ɵij������������������֮��Ĺ�ϵ���±���
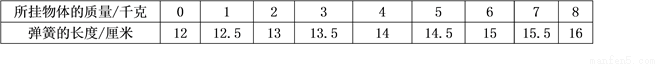
��1���ϱ��У��Ա����� ��������� ��
��2�����ɲ�������ij����� ��
��3�������x��ʾ���������������������y��ʾ���ɵij��ȣ���ô����x�ı仯��y�ı仯������ ��д��y��x�Ĺ�ϵʽ ��
��4�����������������Ϊ25ǧ�ˣ����ܼ����������Ϊ14ǧ��ʱ�����ɵij����Ƕ��٣�
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ����������ODBC�У���OC=1��OA=OB���������ϵ�A��ʾ������__________��
ij��һ����ˮ1890mL�����������뷨��1890mL��ȷ��1000mL��ʾΪ____mL��
�鿴����ƽ��ֱ������ϵ�У��㣨2��-3���ڵ�____���ޣ�
�鿴��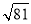 ��ƽ����Ϊ_____��
��ƽ����Ϊ_____��
����ֱ��l:y=kx+k(k��0),����˵������ȷ����(��)
A. ��(0,k)��l��
B. l��������(-1,0)
C. ��k>0ʱ,y��x�����������
D. l������һ������������
�鿴����ͼ��һ�κ���y1��x��b��һ�κ���y2��kx��4��ͼ���ڵ�P��1��3���������x�IJ���ʽx��b��kx��4�Ľ⼯�ǣ�������
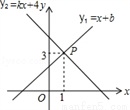
A. x����2 B. x��0 C. x��1 D. x��1
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������