10. 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )| A. | $\sqrt{23}$ | B. | $\sqrt{13}$ | C. | $\sqrt{17}$ | D. | $\sqrt{26}$ |
9.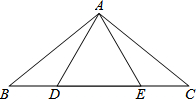 如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
 如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )| A. | DA=DE | B. | AD=AE | C. | BC=CE | D. | BE=CD |
7.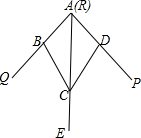 如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
 如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=CD,BC=DC,将仪器上的点与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )| A. | SSS | B. | ASA | C. | AAS | D. | SAS |
1.设a=$\sqrt{11}$+1,a在两个相邻整数之间,则这两个整数是( )
0 312120 312128 312134 312138 312144 312146 312150 312156 312158 312164 312170 312174 312176 312180 312186 312188 312194 312198 312200 312204 312206 312210 312212 312214 312215 312216 312218 312219 312220 312222 312224 312228 312230 312234 312236 312240 312246 312248 312254 312258 312260 312264 312270 312276 312278 312284 312288 312290 312296 312300 312306 312314 366461
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
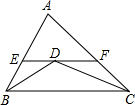 如图,△ABC中,AB=6,AC=8,BD,CD平分∠ABC、∠ACB,过D作平行于BC,交AB、AC于E、F,则△AEF的周长为( )
如图,△ABC中,AB=6,AC=8,BD,CD平分∠ABC、∠ACB,过D作平行于BC,交AB、AC于E、F,则△AEF的周长为( )