题目内容
10. 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )| A. | $\sqrt{23}$ | B. | $\sqrt{13}$ | C. | $\sqrt{17}$ | D. | $\sqrt{26}$ |
分析 过A、C点作l3的垂线构造出直角三角形,根据三角形全等求出BE=AD=2,由勾股定理求出BC的长,再利用勾股定理即可求出.
解答 解:如图,作AD⊥l3于D,作CE⊥l3于E,
∵∠ABC=90°,
∴∠ABD+∠CBE=90°
又∠DAB+∠ABD=90°
∴∠BAD=∠CBE,
在△ABD和△BEC中,$\left\{\begin{array}{l}{∠ADB=∠BEC}\\{∠BAD=∠EBC}\\{AB=BC}\end{array}\right.$
∴△ABD≌△BCE(AAS),
∴BE=AD=2,
在Rt△BCE中,根据勾股定理,得BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{13}$,
在Rt△ABC中,根据勾股定理,得AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{26}$.
故选:D.
点评 本题考查了全等三角形的性质和判定,勾股定理的应用,此题要作出平行线间的距离,构造直角三角形.运用全等三角形的判定和性质以及勾股定理进行计算.

练习册系列答案
相关题目
1.下列说法中正确的是( )
| A. | 4的算术平方根是±2 | B. | -a2一定没有平方根 | ||
| C. | -$\sqrt{5}$表示5的算术平方根的相反数 | D. | 0.9的算术平方根是0.3 |
20.一个数的绝对值是3,那么这个数是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | -$\frac{1}{3}$ |
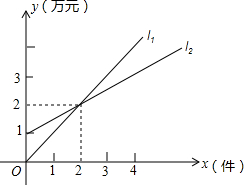 如图,L1表示某公司一种产品一天的销售收入与销售量的关系,L2表示该公司这种产品一天的销售成本与销售量的关系
如图,L1表示某公司一种产品一天的销售收入与销售量的关系,L2表示该公司这种产品一天的销售成本与销售量的关系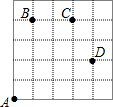 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4).其中第一数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负,如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4).其中第一数表示左右方向,第二个数表示上下方向,那么图中