下列命题中：①若a是实数，则a²＞0；②有两条边和一个角对应相等的两个三角形全等；③两个无理数的和不一定是无理数；④平行于同一条直线的两条直线平行；⑤两条对角线相等的四边形是矩形；⑥若a-b+c=0，则关于x的方程ax²+bx+c=0有一个根为-1．其中正确命题有________（只填序号）．

根据不等式的性质把下列不等式化成x＞a或x＜a的形式．
（1）x+7＞9
（2）6x＜5x-3
（3）．

如果的值是一个整数，且是大于1的数，那么满足条件的最小的整数a=________．

如图，△ABC中，∠ACB=90°，AD⊥AB，AD=AB，BE⊥DC于点E，CA的垂线AF交AB的延长线于点F，连接CF，求∠ACF的度数．

用科学记数法表示602300，应该是

1. A.
   602.3×10³
2. B.
   6023×10²
3. C.
   6.023×10⁵
4. D.
   6.023×10⁶

有一只小猫在房间里面来回走动，右图是房间的地砖，它最后停留在黑色地砖的概率是________．

2006年，衢江区深入实施“811”环境污染整治行动，沈家经济开发区的49家化工企业中已关停33家，每年排放
的污水减少了167900吨．将167900吨用科学记数法（保留三个有效数字）表示的结果为________吨．

如图，从A地到B地共有五条路，你应选择第________条路，因为________．

先阅读短文，再回答短文后面的问题．
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线，点F叫做抛物线的焦点，直线l叫做抛物线的准线．
下面根据抛物线的定义，我们来求抛物线的方程．
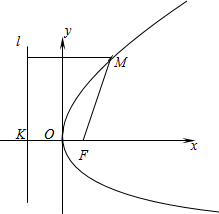
如上图，建立直角坐标系xoy，使x轴经过点F且垂直于直线l，垂足为K，并使原点与线段KF的中点重合．设|KF|=p（p＞0），那么焦点F的坐标为（，0），准线l的方程为x=-．
设点M（x，y）是抛物线上任意一点，点M到l的距离为d，由抛物线的定义，抛物线就是满足|MF|=d的点M的轨迹．
∵|MF|=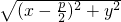，d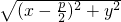=|x+|∴=|x+|
将上式两边平方并化简，得y²=2px（p＞0）①
方程①叫做抛物线的标准方程，它表示的抛物线的焦点在x轴的正半轴上，坐标是（，0），它的准线方程是x=-．
一条抛物线，由于它在坐标平面内的位置不同，方程也不同．所以抛物线的标准方程还有其它的几种形式：y²=-2px，x²=2py，x²=-2py．这四种抛物线的标准方程，焦点坐标以及准线方程列表如下：

标准方程	交点坐标	准线方程
y2=2px（p＞0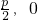）	（）	x=-
y2=-2px（p＞0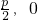）	（-）	x=
x2=2py（p＞0）	（0，）	y=-
x2=-2py（p＞0）	（0，-）	y=-

解答下列问题：
（1）①已知抛物线的标准方程是y²=8x，则它的焦点坐标是______，准线方程是______
②已知抛物线的焦点坐标是F（0，-6），则它的标准方程是______．
（2）点M与点F（4，0）的距离比它到直线l：x+5=0的距离小1，求点M的轨迹方程．
（3）直线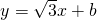经过抛物线y²=4x的焦点，与抛物线相交于两点A、B，求线段AB的长．

若三角形的三边a、b、c满足，则第三边c的取值范围是________．