12．已知矩形的面积为1，设该矩形的长为x，周长为y，小彬借鉴以前研究函数的经验，对函数y随自变量x的变化进行了探究；以下是小彬的探究过程：
（1）结合问题情境分析：
①y与x的函数表达式为y=2x+$\frac{2}{x}$；②自变量x的取值范围是x＞0．
（2）下表是y与x的几组对应值．
①写出m的值；
②画出函数图象；
③观察图象，写出该函数两条不同类型的性质．
（1）结合问题情境分析：
①y与x的函数表达式为y=2x+$\frac{2}{x}$；②自变量x的取值范围是x＞0．
（2）下表是y与x的几组对应值．
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
②画出函数图象；
③观察图象，写出该函数两条不同类型的性质．
已知：如图，在平行四边形ABCD中，延长CB至E，延长AD至F，使得BE=DF，连接EF与对角线AC交于点O．求证：OE=OF．
如图，六边形ABCDEF是正六边形，那么∠α的度数是60°．
甲、乙两人沿相同的路线由A地到B地匀速前进，A、B两地间的路程为20km．他们前进的路程为s（km），甲出发后的时间为t （h），甲、乙前进的路程与时间的函数图象如图所示．①乙比甲晚出发1小时；②甲比乙晚到B地3小时；③甲的速度是5千米/时；④乙的速度是10千米/小时；根据图象信息，下列说法正确的是（ ）
6．若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（ ）
| A． | -9 | B． | -3 | C． | 3 | D． | -3或3 |
5．一个不透明的盒子中装有3个红球，2个黄球和1个白球，这些球除了颜色外无其他差别，从中随机摸出一个小球，恰好是红球的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
4．
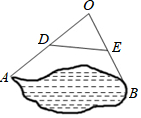如图，为测量池塘边上两点A，B之间的距离，可以在池塘的一侧选取一点O，连接OA，OB，并分别取它们的中点D，E，连接DE，现测出AO=36米，BO=30米，DE=20米，那么A，B间的距离是（ ）
0 297417 297425 297431 297435 297441 297443 297447 297453 297455 297461 297467 297471 297473 297477 297483 297485 297491 297495 297497 297501 297503 297507 297509 297511 297512 297513 297515 297516 297517 297519 297521 297525 297527 297531 297533 297537 297543 297545 297551 297555 297557 297561 297567 297573 297575 297581 297585 297587 297593 297597 297603 297611 366461
如图，为测量池塘边上两点A，B之间的距离，可以在池塘的一侧选取一点O，连接OA，OB，并分别取它们的中点D，E，连接DE，现测出AO=36米，BO=30米，DE=20米，那么A，B间的距离是（ ）| A． | 30米 | B． | 40米 | C． | 60米 | D． | 72米 |
