12.数学问题:在1~51这51个自然数中,每次取两个不同的数,使得所取的两个数之和大于51,有多少中不同取法?
数学模型:为找到解决上面问题的方法,先建立简单的数学模型进行研究:
(1)在1~5这5个自然数中,每次取两个不同的数,使得所取的两个数之和大于5,有多少种不同取法?
解决问题过程如下:
第1行有1种取法(1,5)
第2行有2种取法(2,4),(2,5)
第3行有3种取法(3,3),(3,4),(3,5)
第4行有4种取法(4,2),(4,3),(4,4),(4,5)
第5行有5种取法(5,1),(5,2),(5,3),(5,4),(5,5)
共有1+2+3+4+5种取法,因为每次取两个不同的数,所以在这些取法中不包括(3,3),(4,4),(5,5),要从总数中减去这3中取法,并且(4,2)与(2,4),(4,3)与(3,4),(5,1)与(1,5),(5,2)与(2,5),…(5,4)与(4,5)是同一种取法,因此共有$\frac{1+2+3+4+5-\frac{5+1}{2}}{2}$=6种不同的取法.
(2)在1~6这6个自然数中,每次取两个不同的数,使得所取的两个数之和大于6,有多少种不同的取法?
解决问题过程如下:
第1行有1种取法(1,6)
第2行有2种取法(2,5),(2,6)
第3行有3种取法(3,4),(3,5),(3,6)
第4行有4种取法(4,3),(4,4),(4,5),(4,6)
第5行有5种取法(5,2),(5,3),(5,4),(5,5),(5,6)
第6行有6种取法(6,1),(6,2),(6,3),6,4),(6,5),(6,6)
共有1+2+3+4+5+6种取法,因为每次取两个不同的数,所以在这些取法中不包括(4,4),(5,5),(6,6),要从总数中减去这3中取法,并且(4,3)与(3,4),(5,2)与(2,5),(5,3)与(3,5),(5,4)与(4,5),(6,1)与(1,6),(6,2)与(2,6)…(6,5)与(5,6)是同一种取法,因此共有$\frac{1+2+3+4+5+6-\frac{6}{2}}{2}$=9种不同的取法.
归纳探究:
仿照上述研究问题的思路和解决过程,回答下列提出的问题:
(1)在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有12种不同取法.(只填结果)
(2)在1~8这8个自然数中,每次取两个不同的数,使得所取的两个数之和大于8,共有16种不同取法.(只填结果)
(3)在1~n(n为奇数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}-1}{4}$种不同取法.(只填最简算式)
(4)在1~n(n为偶数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}}{4}$种不同取法.(只填最简算式)
类比应用:类比上述研究方法或应用其结论,解决下列提出的问题:
(5)各边长都是整数,最大边长为51的三角形有多少个?(直接列出算术,并计算结果)
数学模型:为找到解决上面问题的方法,先建立简单的数学模型进行研究:
(1)在1~5这5个自然数中,每次取两个不同的数,使得所取的两个数之和大于5,有多少种不同取法?
解决问题过程如下:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) |
第2行有2种取法(2,4),(2,5)
第3行有3种取法(3,3),(3,4),(3,5)
第4行有4种取法(4,2),(4,3),(4,4),(4,5)
第5行有5种取法(5,1),(5,2),(5,3),(5,4),(5,5)
共有1+2+3+4+5种取法,因为每次取两个不同的数,所以在这些取法中不包括(3,3),(4,4),(5,5),要从总数中减去这3中取法,并且(4,2)与(2,4),(4,3)与(3,4),(5,1)与(1,5),(5,2)与(2,5),…(5,4)与(4,5)是同一种取法,因此共有$\frac{1+2+3+4+5-\frac{5+1}{2}}{2}$=6种不同的取法.
(2)在1~6这6个自然数中,每次取两个不同的数,使得所取的两个数之和大于6,有多少种不同的取法?
解决问题过程如下:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
第2行有2种取法(2,5),(2,6)
第3行有3种取法(3,4),(3,5),(3,6)
第4行有4种取法(4,3),(4,4),(4,5),(4,6)
第5行有5种取法(5,2),(5,3),(5,4),(5,5),(5,6)
第6行有6种取法(6,1),(6,2),(6,3),6,4),(6,5),(6,6)
共有1+2+3+4+5+6种取法,因为每次取两个不同的数,所以在这些取法中不包括(4,4),(5,5),(6,6),要从总数中减去这3中取法,并且(4,3)与(3,4),(5,2)与(2,5),(5,3)与(3,5),(5,4)与(4,5),(6,1)与(1,6),(6,2)与(2,6)…(6,5)与(5,6)是同一种取法,因此共有$\frac{1+2+3+4+5+6-\frac{6}{2}}{2}$=9种不同的取法.
归纳探究:
仿照上述研究问题的思路和解决过程,回答下列提出的问题:
(1)在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有12种不同取法.(只填结果)
(2)在1~8这8个自然数中,每次取两个不同的数,使得所取的两个数之和大于8,共有16种不同取法.(只填结果)
(3)在1~n(n为奇数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}-1}{4}$种不同取法.(只填最简算式)
(4)在1~n(n为偶数)这n个自然数中,每次取两个不同的数,使得所取的两个数之和大于n,共有$\frac{{n}^{2}}{4}$种不同取法.(只填最简算式)
类比应用:类比上述研究方法或应用其结论,解决下列提出的问题:
(5)各边长都是整数,最大边长为51的三角形有多少个?(直接列出算术,并计算结果)
8.下列各式中一定是二次根式的是( )
| A. | $\sqrt{-7}$ | B. | $\root{3}{2m}$ | C. | $\sqrt{{x^2}+1}$ | D. | $\root{3}{{\frac{a}{b}}}$ |
7.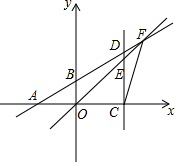 如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
 如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.
如图,点A、B坐标分别为A(-2,0),B(0,1),点E是坐标平面内的任意一点,过点E作x轴的垂线交x轴于点C,交直线AB于点D,直线OE交直线AB于点F,连接CF,若△CEF是一个有一内角为120°的等腰三角形,则符合条件的点E的有( )个.| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
5.下列说法中错误的是( )
| A. | 4的算术平方根是2 | B. | 负数有立方根,并且是负数 | ||
| C. | 8的立方根是±2 | D. | -1的立方根是-1 |
4.下列各式是二次根式的是( )
0 283379 283387 283393 283397 283403 283405 283409 283415 283417 283423 283429 283433 283435 283439 283445 283447 283453 283457 283459 283463 283465 283469 283471 283473 283474 283475 283477 283478 283479 283481 283483 283487 283489 283493 283495 283499 283505 283507 283513 283517 283519 283523 283529 283535 283537 283543 283547 283549 283555 283559 283565 283573 366461
| A. | $\sqrt{2}$ | B. | $\sqrt{m}$ | C. | $\sqrt{-16}$ | D. | $\root{3}{27}$ |


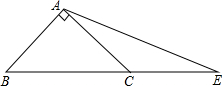 己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.
己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.