14.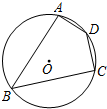 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
0 282820 282828 282834 282838 282844 282846 282850 282856 282858 282864 282870 282874 282876 282880 282886 282888 282894 282898 282900 282904 282906 282910 282912 282914 282915 282916 282918 282919 282920 282922 282924 282928 282930 282934 282936 282940 282946 282948 282954 282958 282960 282964 282970 282976 282978 282984 282988 282990 282996 283000 283006 283014 366461
 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
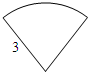 如图,半径为3cm的扇形纸片的周长为10cm,将它围成一个圆锥的侧面,则圆锥的底面圆的半径等于$\frac{2}{π}$cm.(结果保留π)
如图,半径为3cm的扇形纸片的周长为10cm,将它围成一个圆锥的侧面,则圆锥的底面圆的半径等于$\frac{2}{π}$cm.(结果保留π)
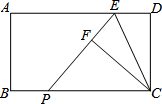 如图,在矩形ABCD中,点E是AD上的点,且tan∠ECD=$\frac{1}{2}$,将△CDE沿CE对折,得到△CEF,延长EF交于BC点P,则sin∠EPC=$\frac{4}{5}$.
如图,在矩形ABCD中,点E是AD上的点,且tan∠ECD=$\frac{1}{2}$,将△CDE沿CE对折,得到△CEF,延长EF交于BC点P,则sin∠EPC=$\frac{4}{5}$. 如图,AB∥CD,AB与EC交于点F,如果EA=EF,∠C=110°,则∠E=40度.
如图,AB∥CD,AB与EC交于点F,如果EA=EF,∠C=110°,则∠E=40度.