题目内容
19.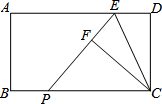 如图,在矩形ABCD中,点E是AD上的点,且tan∠ECD=$\frac{1}{2}$,将△CDE沿CE对折,得到△CEF,延长EF交于BC点P,则sin∠EPC=$\frac{4}{5}$.
如图,在矩形ABCD中,点E是AD上的点,且tan∠ECD=$\frac{1}{2}$,将△CDE沿CE对折,得到△CEF,延长EF交于BC点P,则sin∠EPC=$\frac{4}{5}$.
分析 设ED=1,则CD=2,由折叠性质得:∠DEC=∠CEP,EF=ED=1,CF=CD=2,∠EFC=∠D=90°,得到∠CEP=∠ECP,于是有PC=PE,设PC=PE=x,则PF=x-1,根据勾股定理可求得CP,根据正弦三角函数的定义即可求得结论.
解答 解:∵四边形ABCD是矩形,
∴∠D-90°,AD∥BC,
∴∠DEC=∠ECP,
∵tan∠ECD=$\frac{1}{2}$,
设ED=1,则CD=2,
由折叠性质得:∠DEC=∠CEP,EF=ED=1,CF=CD=2,∠EFC=∠D=90°,
∴∠CEP=∠ECP,
∴PC=PE,
设PC=PE=x,则PF=x-1,
在Rt△PCF中,PC2=PF2+CF2,∴x2=(x-1)2+22,
解得:x=$\frac{5}{2}$,
∴CP=$\frac{5}{2}$,
sin∠EPC=$\frac{CF}{PC}$=$\frac{2}{\frac{5}{2}}$=$\frac{4}{5}$,
故答案为:$\frac{4}{5}$.
点评 本题主要考查了矩形的性质,平行线的性质,三角函数的定义,勾股定理,折叠的性质,能够利用勾股定理和折叠的性质构造方程是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列四个实数中,最小的是( )
| A. | -3 | B. | -π | C. | -$\sqrt{5}$ | D. | 0 |
10.一个多边形的每个内角均为120°,则这个多边形是( )
| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |
7.下列四种正多边形:①正三角形;②正方形;③正五边形;④正六边形,其中既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.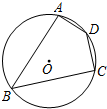 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
 如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )
如图,四边形ABCD内接于⊙O.若⊙O的半径为4,∠D=135°,则$\widehat{AC}$的长为( )| A. | π | B. | 2π | C. | 4π | D. | 8π |
9.若关于x的方程x2+3x+a=0有一个根为1,则另一个根为( )
| A. | -4 | B. | 2 | C. | 4 | D. | -3 |
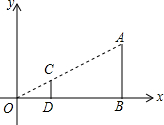 在直角坐标系中有两点A(6,3)、B(6,0).以原点O为位似中心,把线段AB按相似的1:3缩小后得到线段CD,点C在第一象限(如图),则点C的坐标为(2,1).
在直角坐标系中有两点A(6,3)、B(6,0).以原点O为位似中心,把线段AB按相似的1:3缩小后得到线段CD,点C在第一象限(如图),则点C的坐标为(2,1).