3. 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )| A. | ∠ACD=120° | B. | ∠ACD=∠BCE | C. | ∠ACE=120° | D. | ∠ACE-∠BCD=120° |
2.已知$\frac{x}{y}$=$\frac{3}{2}$,那么下列等式中一定正确的是( )
| A. | $\frac{3x}{y}$=$\frac{9}{2}$ | B. | $\frac{x+3}{y+3}$=$\frac{6}{5}$ | C. | $\frac{x-3}{y-2}$=$\frac{3}{2}$$•\frac{x}{y}$ | D. | $\frac{x+y}{x}$=$\frac{5}{2}$ |
1.在平面直角坐标系中,点A(a,a),以点B(0,4)为圆心,半径为1的圆上有一点C,直线AC与⊙B相切,切点为C,则线段AC的最小值为( )
| A. | 3 | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{7}$-1 |
20. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a+b)(a-2b)=a2-ab-2b2 |
18.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2;
(2)一个多面体的棱数比顶点数大10,且有12个面,则这个多面体的棱数是30;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.
0 279705 279713 279719 279723 279729 279731 279735 279741 279743 279749 279755 279759 279761 279765 279771 279773 279779 279783 279785 279789 279791 279795 279797 279799 279800 279801 279803 279804 279805 279807 279809 279813 279815 279819 279821 279825 279831 279833 279839 279843 279845 279849 279855 279861 279863 279869 279873 279875 279881 279885 279891 279899 366461

(1)根据上面多面体的模型,完成表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
(2)一个多面体的棱数比顶点数大10,且有12个面,则这个多面体的棱数是30;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,每个顶点处都有3条棱,共有棱36条.若该多面体外表面三角形的个数比八边形的个数的2倍多2,求该多面体外表面三角形的个数.
 如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为( )
如图,在等边△ABC中,AC=4,点D、E、F分别在三边AB、BC、AC上,且AF=1,FD⊥DE,∠DFE=60°,则AD的长为( )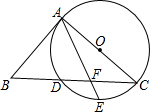 如图,AC是⊙O的直径,BC交⊙O于点D,E是$\widehat{CD}$的中点,连接AE交BC于点F,∠ABC=2∠EAC.
如图,AC是⊙O的直径,BC交⊙O于点D,E是$\widehat{CD}$的中点,连接AE交BC于点F,∠ABC=2∠EAC.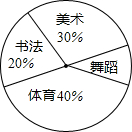 某校为了解学生的课余爱好,对全校1200名学生进行抽样调查,并把调查结果制成如图所示的统计图,由图可知,该校喜欢舞蹈的学生大约有120名.
某校为了解学生的课余爱好,对全校1200名学生进行抽样调查,并把调查结果制成如图所示的统计图,由图可知,该校喜欢舞蹈的学生大约有120名.