18．在正方形ABCD中.AB=10cm.对角线AC.BD相交于O.则△ABO的周长是( )A．10+5$\sqrt{2}$B．10+$\sqrt{2}$C．20+5$\sqrt{2}$D．10+10——青夏教育精英家教网——

18．在正方形ABCD中，AB=10cm，对角线AC、BD相交于O，则△ABO的周长是（　　）

10+10$\sqrt{2}$

17．已知一口袋中放有红、白、黑三种颜色的球共50个，它们除颜色外其他都一样，一位同学通过多次试验后发现摸到红、白色的频率基本稳定是45%和15%，则袋中黑球的个数可能是（　　）

16．用配方法解方程x²-2x-6=0时，原方程应变形为（　　）

15．同时掷两枚骰子，和是7的概率是（　　）

14．下列方程中，是关于x的一元二次方程的是（　　）

（x+2）（x+1）=x²

$\frac{1}{x^2}+\frac{1}{x}$-2=0

13．国强同学喜欢用黑色棋子摆放在正多边形的边上来研究数的规律．请你观察下面表格中棋子的摆放规律，并回答下面问题：

三角形				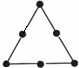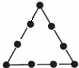…	第n个三角形
棋子个数	3	6	9	…	P
正方形				…	第n个正方形
棋子个数	4	8	12	…	Q
正多边形					第n个正多边形
棋子个数	3	8	15	24	M

（1）通过观察、归纳发现可以分别用含字母n（n≥1的整数）的代数式表示P、Q、M．则P=3n，Q=4n，M=n（n+2）．
（2）下列数中既是三角形中的棋子数又是正方形中的棋子数的是D．
A.2013 B.2014 C.2015 D.2016．

12．阅读理解题：
如图，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．

（1）可求得x=9，第2015个格子中的数为-6；
（2）判断：前n个格子中所填整数之和是否可能为2015？若能，求出n的值，若不能，请说明理由；
（3）若取前3格子中的任意两个数，记作a、b，且a≥b，那么所有的|a-b|的和可以通过计算|9-★|+|9-☆|+|☆-★|得到．其结果为30；若取前19格子中的任意两个数，记作s、t，且s≥t，求所有的|s-t|的和．

11．探究题：
下图是某月的月历．

（1）如图1，带阴影的方框中的9个数之和是99；
（2）如果将带阴影的方框移至图2的位置，则这9个数之和是144；
（3）如果将带阴影的方框移至9个数之和为198的位置，求这9个数中最小的数．

有理数a，b在数轴上的对应点位置如图所示，
（1）用“＜”连接0，a，b，-1；
（2）化简：|a|+|a+b|-2|b-a|．

9．解方程：
（1）2（x-3）-5（3-x）=21
（2）$\frac{2-x}{3}$-$\frac{3（x-1）}{2}$=4．

0 279011 279019 279025 279029 279035 279037 279041 279047 279049 279055 279061 279065 279067 279071 279077 279079 279085 279089 279091 279095 279097 279101 279103 279105 279106 279107 279109 279110 279111 279113 279115 279119 279121 279125 279127 279131 279137 279139 279145 279149 279151 279155 279161 279167 279169 279175 279179 279181 279187 279191 279197 279205 366461