如图,正方形网格中的每个小正方形的边长都是 1,每个顶点叫做格
点.
|
|
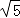
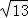 ;这个三角形的面积为 2 .
;这个三角形的面积为 2 . 如图,正方形网格中的每个小正方形的边长都是 1,每个顶点叫做格
点.
|
|
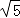
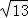 ;这个三角形的面积为 2 .
;这个三角形的面积为 2 .