题目内容
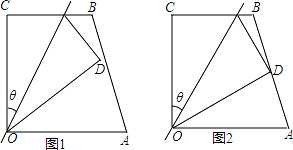
如图 1,四边形 OABC 中,OA=a,OC=8,∠AOC=∠BCO=90°,经过点 O 的直线 l 将四边形分 成两部分,直线 l 与 OC 所成的角设为 θ,将四边形 OABC 的直角∠OCB 沿直线 l 折叠,点 C 落在 点 D 处(如图 1).
(1)若点 D 与点 A 重合,则 θ= ,a= ; 若折叠后点 D 恰为 AB 的中点(如图 2),求 θ 的度数.
【考点】翻折变换(折叠问题).
【分析】(1)利用轴对称的性质即可解决问题;
延长 MD、OA,交于点 N,如图 2.易证△BDM≌△ADN,则有 DM=DN,根据垂直平分线的性质 可得 OM=ON,根据等腰三角形的性质可得∠MOD=∠NOD,从而就可求出 θ.
【解答】解:(1)若点 D 与点 A 重合, 则 θ=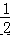 ∠COA=45°,OA=OC=8.
∠COA=45°,OA=OC=8.
故答案为:45°,8.
如图:延长 MD、OA,交于点 N.
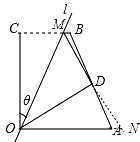
∵∠AOC=∠BCO=90°,
∴∠AOC+∠BCO=180°,
∴BC∥OA,
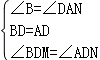 ∴∠B=∠DAN. 在△BDM 和△AD
∴∠B=∠DAN. 在△BDM 和△AD N 中,
N 中,
,
∴△BDM≌△ADN(ASA),
∴DM=DN.
∵∠ODM=∠OCM=90°,
∴根据线段垂直平分线的性质可得 OM=ON,
∴根据等腰三角形的性质可得∠MOD=∠NOD. 由折叠可得∠MOD=∠MOC=θ,
∴∠COA=3θ=90°,
∴θ=30°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ﹣(﹣1)2﹣( ﹣1)0+
﹣(﹣1)2﹣( ﹣1)0+ B.
B.  C.
C.  D.
D.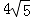 ,△BCE 的面积= .
,△BCE 的面积= .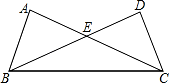
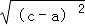 一 2
一 2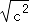 .
.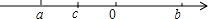
 ,则
,则 等于( ).
等于( ). ,
, ,那么下列说法中错误的是( ).
,那么下列说法中错误的是( ).
 的边
的边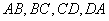 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为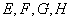 ,顺次连结这四个点,得四边形
,顺次连结这四个点,得四边形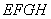 .如图1,当四边形
.如图1,当四边形 ,
,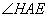 的度数;
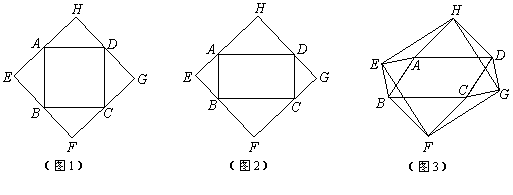
的度数;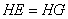 ;
;




 ;
;  (n≥1的整数);
(n≥1的整数); =____________.
=____________.