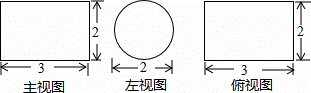
某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为( )
|
| A. | 3π | B. | 2π | C. | π | D. | 12 |
若﹣5x2ym与xny是同类项,则m+n的值为( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
要反映台州市某一周每天的最高气温的变化趋势,宜采用( )
|
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 频数分布统计图 |
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )

|
| A. | 70° | B. | 100° | C. | 140° | D. | 170° |
﹣2014的绝对值是( )
|
| A. | ﹣2014 | B. | 2014 | C. |
| D. | ﹣ |
 |
(1)阅读合作学习内容,请解答其中的问题.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,义乌市某服装厂每件衣服原材料的成本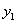 (元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本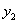 (元)与月份x的函数关系式为
(元)与月份x的函数关系式为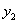 =x+62(8≤x≤12,且x为整数).
=x+62(8≤x≤12,且x为整数).
(1) 请观察表格中的数据,用学过的函数相关知识求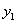 与x的函数关系式.
与x的函数关系式.
(2) 若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量 (万件)与月份x满足关系式
(万件)与月份x满足关系式 =0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量
=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量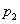 (万件)与月份x满足关系式
(万件)与月份x满足关系式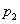 =
= -0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
-0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
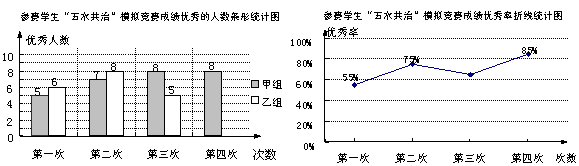
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整.
(2)已求得甲组成绩优秀人数的平均数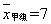 ,方差
,方差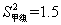 ,请通过计算说明,哪一组成绩优秀的人数较稳定?
,请通过计算说明,哪一组成绩优秀的人数较稳定?

 ②当m=-3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
②当m=-3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.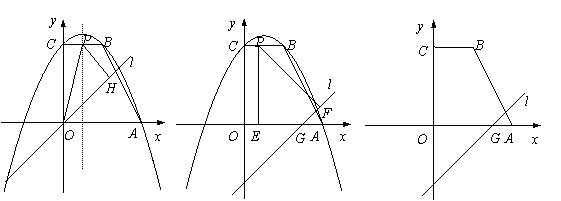
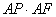 的值.
的值.