��Ŀ����
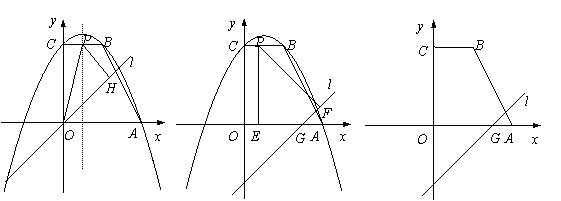
��ͼ��ֱ������ABCO������OA,OC����������������ϣ�BC��x�ᣬOA=OC=4����ֱ��x=1Ϊ�Գ���������߹�A,B,C����.
��1����������ߵĺ�������ʽ.
��2����ֱ֪��l�Ľ���ʽΪy=x+m������x�ύ�ڵ�G��������ABCO��һ����ȡ��P.
�ٵ�m=0ʱ����ͼ1����P�������߶Գ�����BC�Ľ��㣬����P��PH��ֱ��l�ڵ�H,����OP,�����OPH�����.
 �ڵ�m=-3ʱ������P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����Ϊ��E,F.�Ƿ���������ĵ�P,ʹ��P,E,FΪ������������ǵ���������?�����ڣ������P�����ꣻ�������ڣ���˵������.
�ڵ�m=-3ʱ������P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����Ϊ��E,F.�Ƿ���������ĵ�P,ʹ��P,E,FΪ������������ǵ���������?�����ڣ������P�����ꣻ�������ڣ���˵������.
|
��1���������ߵĽ���ʽΪ ���ɶԳ���x=1���ɵõ�B����(2��4)��
���ɶԳ���x=1���ɵõ�B����(2��4)��
�� ���
��� ��
�� .
.
��2����PH��ֱ��l����ON=MN=1��PM=3��
�ɡ�PMHΪ����ֱ�������ε�HM=PH= ,
,
���ԣ� .
.
�ڴ������������
����P�ڱ�OC��ʱ(��ͼ2)����ʱ��E���O�غϣ�
|

ʵ���� ���෴���ǣ�������
���෴���ǣ�������
| �� | A�� | ��2 | B�� |
| C�� | 2 | D�� | ��|��0.5| |
����ͨ������ͶƱѡ����һ��������Т�ĵ������ꡱ�����ݸ�����������ѡ�������������ͳ�Ʊ����������֣�ͳ�Ʊ���ǰ���е��������ݶ�����ȷ�ģ�����������һ�������Ǵ���ģ���ش��������⣺
��1��ͳ�Ʊ���a=��0.1����b=��6����
��2��ͳ�Ʊ�����������һ�������Ǵ���ģ������ݵ���ȷֵ�Ƕ��٣�
��3�������о��������������ص�4λ������Т�ĵ������ꡱ�У���ѡ��λ��Ϊ�м���������ˣ�A��B�������ء�����Т�ĵ������ꡱ�е���λ����A��Bͬʱ��ѡ�ĸ����Ƕ��٣�
| ���� | Ƶ�� | Ƶ�� |
| ������ | 4 | a |
| ������ | 5 | 0.125 |
| ���� | b | 0.15 |
| ������ | 8 | 0.2 |
| ������ | 5 | 0.125 |
| ������� | 12 | 0.25 |
ij�����������ͼ������ͼ����ͼ�ֱ���ͼ����ü���������Ϊ��������
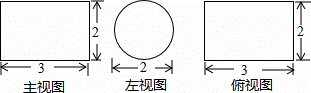
| �� | A�� | 3�� | B�� | 2�� | C�� | �� | D�� | 12 |
����������ȷ���ǣ�������
| �� | A�� | a2+a3=a5 | B�� | ��﹣2a2��3=﹣6a6 | C�� | ��2a+1����2a﹣1��=2a2﹣1 | D�� | ��2a3﹣a2����a2=2a﹣1 |
 �Ľ��� .
�Ľ��� .