Question

等边三角形ABC的边长为6，在AC，BC边上各取一点E,F，  连结AF，BE相交于点P.

（1）若AE=CF.

①求证:AF=BE,并求∠APB的度数.

②若AE=2,试求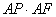的值.

（2）若AF=BE,当点E从点A运动到点C时，试求点P经过的路径长.

Answer 1

（1）①如图，∵△ABC是等边三角形，

  ∴∠C=∠BAC=60°, AB=AC，

又∵AE=CF，

∴△AFC≌△BEA (SAS)，

∴AE=CF,                         

∠1=∠3，

∵∠4=∠2+∠3，

∴∠4=∠2+∠1=∠BAC=60°,

即∠APB=180°-∠4=120°.               

② ∵  ∠C=∠4=60°，∠PAE=∠CAF,

   ∴  △APE∽△ACF,

   ∴，即，所以.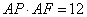  

（2）若AF=BE,有AE=BF或AE=CF两种情况.

当AE=BF时，如图2，此时点P经过的路径是AB边上的高线CH.

    在Rt△AHC中，, 

∴此时点P经过的路径长为.

当AE=CF时，如图3，点P经过的路径是以A，B为端点的        圆弧，且∠APB=120°,则圆心角∠AOB=120°，

 过点O作OG⊥AB, 在Rt△AOG中，∠AOG=60°，

，

∴.

∴此时点P经过的路径长为.

所以，点P经过的路径长为或.