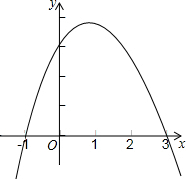
 二次函数y=ax2+bx+c(a、b、c是常数a≠0)的大致图象如图所示,抛物线交x轴于点(-1,0),(3,0).则下列说法中,正确的是( )
二次函数y=ax2+bx+c(a、b、c是常数a≠0)的大致图象如图所示,抛物线交x轴于点(-1,0),(3,0).则下列说法中,正确的是( )| A、abc>0 |
| B、b-2a=0 |
| C、3a+c>0 |
| D、9a+6b+4c>0 |
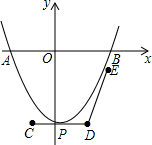 如图,一条抛物线与x轴交于A、B两点,且顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,-4),(2,-4),(3,-1),点A的横坐标的最小值为-3,则点B的横坐标的最大值为( )
如图,一条抛物线与x轴交于A、B两点,且顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,-4),(2,-4),(3,-1),点A的横坐标的最小值为-3,则点B的横坐标的最大值为( )| A、1 | B、2 | C、3 | D、4 |
 如图,已知Rt△ABC,∠C=90°,CA=3,CB=4,点M从点B出发沿线段BC匀速运动至点C,过点M作MN⊥AB于N,则△BMN面积S与点M的运动时间t之间的函数图象大致是( )
如图,已知Rt△ABC,∠C=90°,CA=3,CB=4,点M从点B出发沿线段BC匀速运动至点C,过点M作MN⊥AB于N,则△BMN面积S与点M的运动时间t之间的函数图象大致是( )A、 |
B、 |
C、 |
D、 |
 如图正方形AOBC,等腰Rt△EOF中,∠EOF=90°,EF与OB交于G,连接AE、AB、BF.
如图正方形AOBC,等腰Rt△EOF中,∠EOF=90°,EF与OB交于G,连接AE、AB、BF.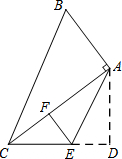 如图,在四边形ABCD中,∠D=90°,∠B=60°,AD=6,AB=
如图,在四边形ABCD中,∠D=90°,∠B=60°,AD=6,AB= 如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.
如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G.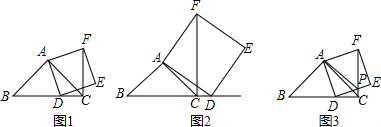

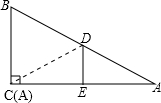 如图,在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ABC沿DE折叠,使得点A与点C重合,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ABC沿DE折叠,使得点A与点C重合,则折痕DE的长为( )