设点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C( )
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、既关于x轴对称,又关于y轴对称 |
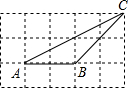 如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )
如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、既关于x轴对称,又关于y轴对称 |
 如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )
如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|