题目内容
某工厂使用旧设备生产,每月生产收入是90万元,每月另需支付设备维护费5万元,从今年1月份起使用新设备,生产收入提高且无设备维护费,使用当月生产收入达100万元,1至3月份生产收入以相同的百分率逐月增长,累计达364万元,3月份后,每月生产收入稳定在3月份的水平.
(1)求使用新设备后,2月、3月生产收入的月增长率;
(2)购进新设备需一次性支付640万元,使用新设备几个月后,该厂所得累计利润不低于使用旧设备的累计利润?(累计利润是指累计生产收入减去就设备维护费或新设备购进费)
(1)求使用新设备后,2月、3月生产收入的月增长率;
(2)购进新设备需一次性支付640万元,使用新设备几个月后,该厂所得累计利润不低于使用旧设备的累计利润?(累计利润是指累计生产收入减去就设备维护费或新设备购进费)
考点:一元二次方程的应用,一元一次不等式的应用
专题:增长率问题
分析:(1)设每月的增长率为x,那么2月份的生产收入为100(1+x),三月份的生产收入为100(1+x)2,根据1至3月份的生产收入累计可达364万元,可列方程求解.
(2)设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,根据不等关系可列不等式求解.
(2)设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,根据不等关系可列不等式求解.
解答:解:(1)设每月的增长率为x,由题意得:
100+100(1+x)+100(1+x)2=364,
解得x=0.2,或x=-3.2(不合题意舍去)
答:每月的增长率是20%.
(2)设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,依题意有
364+100(1+20%)2(y-3)-640≥(90-5)y,
解得y≥12.
故使用新设备12个月后,该厂所得累计利润不低于使用旧设备的累计利润.
100+100(1+x)+100(1+x)2=364,
解得x=0.2,或x=-3.2(不合题意舍去)
答:每月的增长率是20%.
(2)设使用新设备y个月后,该厂所得累计利润不低于使用旧设备的累计利润,依题意有
364+100(1+20%)2(y-3)-640≥(90-5)y,
解得y≥12.
故使用新设备12个月后,该厂所得累计利润不低于使用旧设备的累计利润.
点评:本题考查理一元二次方程的应用和解题能力,关键是找到1至3月份的生产收入累计可达100万元和不等量关系可列方程和不等式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式
x<6的解集在数轴上表示正确的是( )
| 2 |
| 3 |
A、 |
B、 |
C、 |
D、 |
已知(x3-mx2+nx-2)÷(x-2)的商为x2-3x+1,余式为0,那么m-n的值为( )
| A、-12 | B、-2 | C、12 | D、2 |
 如图是由一些相同的小正方体构成的立体图形的三种视图,那么构成这个立体图形的小正方体有
如图是由一些相同的小正方体构成的立体图形的三种视图,那么构成这个立体图形的小正方体有 如图,△ABC中,点D在BC上,EF∥BC,分别交AB、AC、AD于点E、F、G,已知AE=4,CF=3,
如图,△ABC中,点D在BC上,EF∥BC,分别交AB、AC、AD于点E、F、G,已知AE=4,CF=3,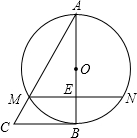 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=
如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=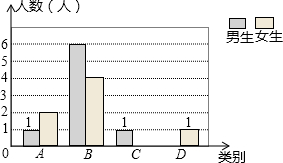 某校九年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表:
某校九年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表: