题目内容
如图,在平面直角坐标系中,双曲线y= 与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y=
与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y= 相交于点E、F,并使得双曲线y=
相交于点E、F,并使得双曲线y=  ,y=
,y= ,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则点A、点E、点B、点F构成的四边形的面积是多少?(用含k的代数式表示)
,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则点A、点E、点B、点F构成的四边形的面积是多少?(用含k的代数式表示)

解:∵ ∴
∴ 
把点A(1,1)代入y=kx+b中得:1=k+b
 ∴b=1-k ∴y=kx+(1-k)
∴b=1-k ∴y=kx+(1-k)
由 得
得

∴
 ∴点B的坐标为
∴点B的坐标为
由双曲线y= 与y=
与y= 与直线y=kx+b以及新直线的对称性可得:
与直线y=kx+b以及新直线的对称性可得:
点A与点E关于y轴对称,点B与点F关于y轴对称,
∴E(-1,1)、F
∴AE=2,BF= ,AE与BF的距离为k+1
,AE与BF的距离为k+1
∴梯形


练习册系列答案
相关题目
 元,买x本笔记本需要
元,买x本笔记本需要 元;求
元;求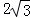 ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: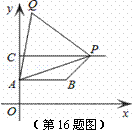
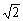 ,则BF=2;正确的结论有( )
,则BF=2;正确的结论有( )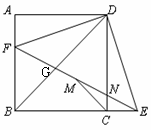
 。
。  (C)
(C)  (D)
(D) 

 B.
B. C.
C.  D.
D.
