题目内容
为表彰在“学雷锋日”活动中表现积极的同学,老师决定购买文具盒与笔记本作为奖品。已知5个文具盒、2本笔记本共需100元;4个文具盒、7本笔记本共需161元。
(1)每个文具盒、每本笔记本各多少元?
(2)商店为了回笼资金,举行“优惠促销”活动,具体办法如下:文具盒“九折”优惠;笔记本10本以上超出部分“八折”优惠.若买x个文具盒需要 元,买x本笔记本需要
元,买x本笔记本需要 元;求
元;求 、
、 关于x的函数关系式;
关于x的函数关系式;
(3)若购买同一种奖品,并且该奖品的数量超过10件,请你分析买哪种奖品省钱。
(1)设每个文具盒x元,每本笔记本y元,可列方程组得
 ,解之得
,解之得
答:每个文具盒14元,每支笔记本15元.
(2)由题意知,y1关于x的函数关系式为y1=14×90%x,即y1=12.6x.
由题意知,买笔记本10以下(含10支)没有优惠,故此时的函数关系式为y2=15x.
当买10支以上时,超出部分有优惠,故此时函数关系式为y2=15×10+15×80%(x-10)
即y2=12x+30
(3)当y1< y2即12.6x<12x+30时,解得x<50;
当y1= y2即12.6x=12x+30时,解得x=50;
当y1> y2即12.6x>12x+30时,解得x>50.
综上所述,当购买奖品超过10件但少于50件时,买文具盒省钱;当购买奖品超过50件时,买文具盒和买笔记本钱数相等;当购买奖品超过50件时,买笔记本省钱.

读一读:式子“1+2+3+4+……+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 ,这里“
,这里“ ”是求和符号,通过以上材料的阅读,计算
”是求和符号,通过以上材料的阅读,计算 = ______
= ______
下列数据是2014年2月7日6点公布的中国六大城市的空气污染指数情况:
| 城市 | 北京 | 合肥 | 南京 | 哈尔滨 | 成都 | 南昌 |
| 污染指数 | 342 | 163 | 165 | 45 | 227 | 163 |
则这组数据的中位数和众数分别是( )
A.164和163 B.105和163 C.105和164 D.163和164
 (3)针对随机调查的情况,小慧决定从初三一班表示赞成的3位家长(其中包含小亮和小丁的家长)中随机选择2位进行深入调查,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
(3)针对随机调查的情况,小慧决定从初三一班表示赞成的3位家长(其中包含小亮和小丁的家长)中随机选择2位进行深入调查,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.

 经过点M(-1,2)和点 N(1,-2),交x 轴于A,B两点,交y轴于C则①
经过点M(-1,2)和点 N(1,-2),交x 轴于A,B两点,交y轴于C则① ;②无论
;②无论 取何值,此二次函数图象与
取何值,此二次函数图象与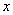 轴必有两个交点,函数图象截
轴必有两个交点,函数图象截 时,
时, 随
随 时,
时, ⑤若
⑤若 以上说法正确的有:( )
以上说法正确的有:( ) 与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y=
与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y= 相交于点E、F,并使得双曲线y=
相交于点E、F,并使得双曲线y= 