题目内容
20．已知函数y=2（x+1）2+1，当x＞-1时，y随x的增大而增大．分析 先求对称轴，再利用函数值在对称轴左右的增减性可得x的范围．
解答 解：函数y=2（x+1）2+1的对称轴是x=-1，
∵a=2＞0，
∴函数图象开口向上，
∴当x＞-1时，函数值y随x的增大而增大．
故答案为：-1．
点评 此题考查二次函数的性质，掌握函数的增减性和求抛物线的对称轴和顶点坐标的方法是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．我们已经研究了“圆周角”，并且知道圆周角的角度等于它所对弧的度数的一半，如图1，∠A=$\frac{\widehat{BC}的度数}{2}$．现将研究对象“顶点在圆上的角”改为“顶点在圆外的角”．定义：顶点在圆外，并且两边都和圆有公共点的角叫做圆外角，例如：图2，∠P为圆外角．
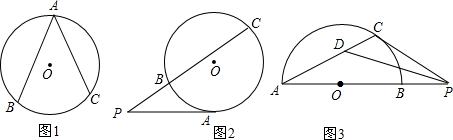
（1）如果以圆外角的两边与圆的公共点的个数作为分类标准，参照图2，请画出其它类型圆外角的示意图（要求：（请按需要选择下面的备用图，每一种类型画出一个示意图，标示相应字母，与图2同类型的不用再画）
（2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
（3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
（4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．
 ∠P=$\frac{\widehat{AmB}的度数-\widehat{AB}的度数}{2}$ | ∠P=$\frac{\widehat{AC}的度数-\widehat{AB}的度数}{2}$ | ∠P=$\frac{\widehat{CD}的度数-\widehat{AB}的度数}{2}$ |
（2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
（3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
（4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．
15．下列说法中，正确的是（ ）
| A． | S=ab是代数式 | |
| B． | a，0，$\frac{2x}{3}$，$\frac{1}{x}$都是单项式 | |
| C． | 单项式和多项式都是整式 | |
| D． | 多项式a2-3ab+2b2是由a2，3ab，2b2组成 |
12．A为反比例函数$y=\frac{k}{x}$（k＜0）图象上一点，AB垂直x轴，垂足为B点，若S△AOB=3，则k的值为（ ）
| A． | 6 | B． | -6 | C． | $\frac{3}{2}$ | D． | 不能确定 |