题目内容
8.菱形ABCD的对角线AC、BD交于点O,∠BAD=120°,AC=4,则它的面积是( )| A. | 16 $\sqrt{3}$ | B. | 8 | C. | 16 | D. | 8 $\sqrt{3}$ |
分析 首先由四边形ABCD是菱形,求得AC⊥BD,OA=$\frac{1}{2}$AC,∠BAC=$\frac{1}{2}$∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2,∠BAC=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB=2$\sqrt{3}$,
∴BD=2OB=4$\sqrt{3}$,
∴该菱形的面积是:$\frac{1}{2}$AC•BD=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$.
故选D.
点评 此题考查了菱形的性质,直角三角形的性质.解题的关键是注意数形结合与方程思想的应用,注意菱形的面积等于其对角线积的一半.

练习册系列答案
相关题目
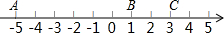 在数轴上有三个点A、B、C,如图所示,请回答:
在数轴上有三个点A、B、C,如图所示,请回答: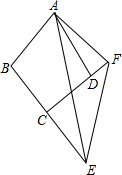 如图.在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,求证:EF=BE-FD.
如图.在四边形ABCD中,∠B+∠ADC=180°,AB=AD,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,求证:EF=BE-FD.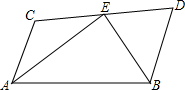 己知AC∥BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E,求证:CE=DE.
己知AC∥BD,∠CAB和∠DBA的平分线EA、EB与CD相交于点E,求证:CE=DE.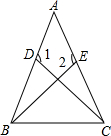 如图,在△ABC中,D,E分别是AB,AC上的点,且AD=AE,CD=BE,∠1=∠2.试判断△ABC的形状,并证明你的判断.
如图,在△ABC中,D,E分别是AB,AC上的点,且AD=AE,CD=BE,∠1=∠2.试判断△ABC的形状,并证明你的判断.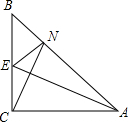 如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.
如图,在△ABC,∠CAB=∠CBA=45°,CA=CB,点E为BC的中点,CN⊥AE交AB于N.