题目内容
3.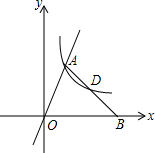 如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)交于A点,B(2,0),连AB交双曲线于D点,且AD=BD,则k=$\frac{8}{9}$.
如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)交于A点,B(2,0),连AB交双曲线于D点,且AD=BD,则k=$\frac{8}{9}$.
分析 过A作AQ⊥y轴于Q,AM⊥x轴于M,过D作DN⊥x轴于N,根据已知得出BN=NM,DN=$\frac{1}{2}$AM,设A(m,n),D(a,b),根据反比例函数系数k的几何意义得出2m=a,从而证得OM=$\frac{1}{3}$OB=$\frac{2}{3}$,求得A的横坐标,代入一次函数解析式得出A的坐标,即可求得k的值.
解答 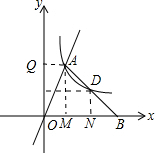 解:过A作AQ⊥y轴于Q,AM⊥x轴于M,过D作DN⊥x轴于N,
解:过A作AQ⊥y轴于Q,AM⊥x轴于M,过D作DN⊥x轴于N,
则AM∥DN,
∵AD=BD,
∴BN=NM,DN=$\frac{1}{2}$AM,
∵B(2,0),
设A(m,n),D(a,b)
∵A、D都在反比例函数y=$\frac{k}{x}$(x>0)上,
∴mn=ab,
∵D的纵坐标为b=$\frac{1}{2}$n,
∴2m=a,
即OM=MN,
∴OM=MN=BN,
∴OM=$\frac{1}{3}$OB=$\frac{2}{3}$,
把x=$\frac{2}{3}$代入y=2x,得y=$\frac{4}{3}$,
∴k=$\frac{2}{3}$×$\frac{4}{3}$=$\frac{8}{9}$.
故答案为:$\frac{8}{9}$.
点评 本题考查了用待定系数法求出反比例函数的解析式,反比例函数系数k的几何意义,三角形的中位线等知识点的应用,主要考查学生的分析能力,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
13.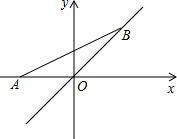 如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0)点B(a,a),当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | D. | (-$\frac{1}{2}$,-$\frac{1}{2}$) |
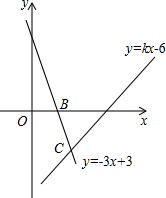 如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.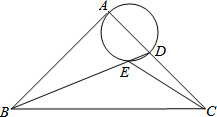 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=$4\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为2$\sqrt{5}$-2.
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=$4\sqrt{2}$,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为2$\sqrt{5}$-2.


