题目内容
14.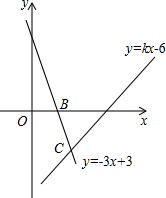 如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.(1)求k的值;
(2)求△ABC的面积;
(3)若点P(0,m)是y轴上的一个动点,当PB+PC的值最小时,求m的值.
分析 (1)直接把A点坐标代入y=kx-6可求出k的值;
(2)通过解方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x-6}\\{y=-3x+3}\end{array}\right.$得C点坐标,再确定B点坐标,然后根据三角形面积公式求解;
(3)作B点关于y轴的对称点D,则D(-1,0),连结CD交y轴于P点,连结PB,由于PB=PD,则PB+PC=PD+PC=CD,根据两点之间线段最短,即可得到此时PB+PC的值最小,再利用待定系数法求出直线CD的解析式,然后计算自变量为0时的函数值即可得到m的值.
解答  解:(1)把A(4,0)代入y=kx-6得4k-6=0,解得k=$\frac{3}{2}$;
解:(1)把A(4,0)代入y=kx-6得4k-6=0,解得k=$\frac{3}{2}$;
(2)解方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x-6}\\{y=-3x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,则C点坐标为(2,-3),
当y=0时,-3x+3=0,解得x=1,则B(1,0),
所以△ABC的面积=$\frac{1}{2}$×(4-1)×3=$\frac{9}{2}$;
(3)作B点关于y轴的对称点D,则D(-1,0),
连结CD交y轴于P点,连结PB,
由于PB=PD,则PB+PC=PD+PC=CD.所以此时PB+PC的值最小,
设直线CD的解析式为y=ax+b,
把C(2,-3),D(-1,0)代入得$\left\{\begin{array}{l}{2a+b=-3}\\{-a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-1}\end{array}\right.$,
所以直线CD的解析式为y=-x-1,
把P(0,m)代入得m=0-1=-1,
即m的值为-1.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了最短路径问题.

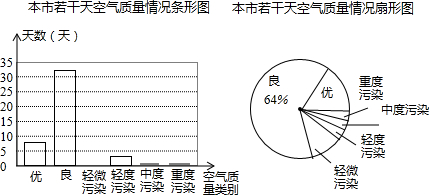
根据以上信息,如下结论错误的是( )
| A. | 被抽取的天数为50天 | |
| B. | 空气轻微污染的所占比例为10% | |
| C. | 扇形统计图中表示优的扇形的圆心角度数57.6° | |
| D. | 估计该市这一年(365天)达到优和良的总天数不多于290天 |
| A. | a≤2 | B. | a≤4 | C. | 2≤a≤4 | D. | a≥2 |
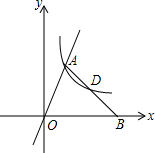 如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)交于A点,B(2,0),连AB交双曲线于D点,且AD=BD,则k=$\frac{8}{9}$.
如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)交于A点,B(2,0),连AB交双曲线于D点,且AD=BD,则k=$\frac{8}{9}$.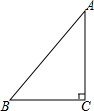 在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系: