题目内容
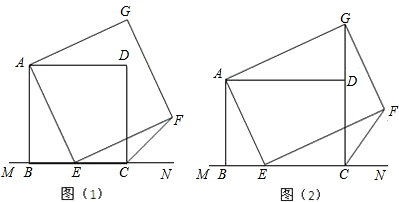
 如图,BE、BD是△ABC中∠ABC的内、外角平分线,AD⊥BD于D,AE⊥BE于E,交BC的延长线于F.
如图,BE、BD是△ABC中∠ABC的内、外角平分线,AD⊥BD于D,AE⊥BE于E,交BC的延长线于F.(1)判断四边形ADBE的形状,并说明理由.
(2)DE与BF相等吗?为什么?
(3)当△ABC满足什么条件时,四边形ADBE是一个正方形?并给出证明.
考点:正方形的判定,矩形的判定与性质
专题:几何图形问题
分析:(1)利用矩形的判定方法得出∠DBE=∠ADB=∠AEB=90°,即可得出答案;
(2)利用矩形的性质以及全等三角形的判定得出AB=BF,进而得出答案;
(3)利用等腰直角三角形的性质以及正方形的判定得出即可.
(2)利用矩形的性质以及全等三角形的判定得出AB=BF,进而得出答案;
(3)利用等腰直角三角形的性质以及正方形的判定得出即可.
解答:解:(1)四边形ADBE是矩形;
理由:∵BE、BD是△ABC中∠ABC的内、外角平分线,
∴∠DBE=
×180°=90°,
∵AD⊥BD于D,AE⊥BE于E,
∴∠ADB=∠AEB=90°,
则∠DBE=∠ADB=∠AEB=90°,
∴四边形ADBE是矩形;
(2)DE=BF,
理由:在△ABE和△FBE中,
,
∴△ABE≌△FBE(ASA),
∴AB=BF,
∵四边形ADBE是矩形,
∴DE=AB,
∴DE=BF;
(3)△ABC为等腰直角三角形时,四边形ADBE是一个正方形,
理由:∵四边形ADBE是矩形,
∴当AE=BE时,四边形ADBE是一个正方形,
∴△ABC为等腰直角三角形时,AB=BC,∠ABC=90°,
则BE=AE=EC,
∴矩形ADBE是正方形.
理由:∵BE、BD是△ABC中∠ABC的内、外角平分线,
∴∠DBE=
| 1 |
| 2 |
∵AD⊥BD于D,AE⊥BE于E,
∴∠ADB=∠AEB=90°,
则∠DBE=∠ADB=∠AEB=90°,
∴四边形ADBE是矩形;
(2)DE=BF,
理由:在△ABE和△FBE中,
|
∴△ABE≌△FBE(ASA),
∴AB=BF,
∵四边形ADBE是矩形,
∴DE=AB,
∴DE=BF;
(3)△ABC为等腰直角三角形时,四边形ADBE是一个正方形,
理由:∵四边形ADBE是矩形,

∴当AE=BE时,四边形ADBE是一个正方形,
∴△ABC为等腰直角三角形时,AB=BC,∠ABC=90°,
则BE=AE=EC,
∴矩形ADBE是正方形.
点评:此题主要考查了矩形的判定与性质以及正方形的判定和全等三角形的判定与性质,正确区分矩形与正方形的判定是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在下面的横线上填上推理的根据,
在下面的横线上填上推理的根据, 一个山坡的倾斜角为10°,坡上有一棵树AB,当阳光与水平线成50°角时,树影BC的长为6米,求树高AB.
一个山坡的倾斜角为10°,坡上有一棵树AB,当阳光与水平线成50°角时,树影BC的长为6米,求树高AB. 如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.