题目内容
10．
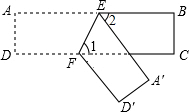如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应．若∠1=65°，则∠2=50°．
分析 由折叠可知∠3=∠4=∠1，可求得∠AEA′，再利用邻补角的定义可求得∠2．
解答 
解：由题意可知∠3=∠4，
∵AB∥CD，
∴∠3=∠4=∠1=65°，
∴∠2=180°-65°-65°=50°，
故答案为：50．
点评 本题主要考查平行线的性质，掌握平行线的判定和性质是解题的关键，即①同位角相等?两直线平行，②内错角相等?两直线平行，③同旁内角互补?两直线平行，④a∥b，b∥c⇒a∥c．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
5．若a=$\frac{1}{b}$-$\frac{1}{c}$，则c=（ ）
| A． | $\frac{1+ab}{b}$ | B． | b-$\frac{1}{a}$ | C． | b+$\frac{1}{a}$ | D． | $\frac{b}{1-ab}$ |
1．某企业为了增收节支，设计了一款成本为20元∕件的工艺品投放市场进行试销．经过调查，得到如下数据：
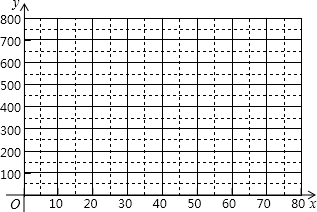
（1）把上表中x、y的各组对应值作为点的坐标，在如图所示的平面直角坐标系中描出相应的点，猜想y与x之间的函数关系式，并求出函数关系式；
（2）市物价部门规定，销售部门规定该工艺品单价不得超过48元，要想每天获得8750元利润，单价应定为多少元？（利润=销售总价-成本总价 ）
| 销售单价x元/件 | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y件 | … | 500 | 400 | 300 | 200 | 100 | … |
（1）把上表中x、y的各组对应值作为点的坐标，在如图所示的平面直角坐标系中描出相应的点，猜想y与x之间的函数关系式，并求出函数关系式；
（2）市物价部门规定，销售部门规定该工艺品单价不得超过48元，要想每天获得8750元利润，单价应定为多少元？（利润=销售总价-成本总价 ）
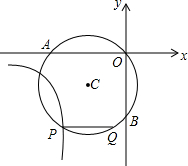如图，过原点O的⊙C与两坐标轴分别交于点A（-4，0）、B（0，-3），在第三象限的⊙C上有一点P，过点P作弦PQ∥x轴，且PQ=3，已知双曲线y=$\frac{k}{x}$过点P，则k的值是$\frac{49}{4}$．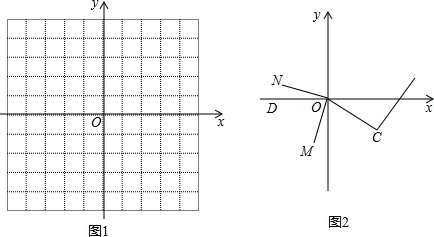
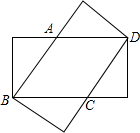如图，四边形EBGD和四边形BFDH是两个全等的矩形，其中ED、BH交于点A，BG、FD交于点C．
2．已知函数y=$\frac{k}{x}$的图象经过点（-1，2），则y=kx的图象（ ）
| A． | 在一、三象限 | B． | 在一、二象限 | C． | 在二、三象限 | D． | 在二、四象限 |
