题目内容
5.在平面直角坐标系中,A、B两点的坐标分别为A(1,a)、B(b,1),且实数a、b满足$\sqrt{a-3}$+$\sqrt{-(4-b)^{2}}$=0.(1)求a,b的值;
(2)平移线段AB至线段PQ处(A的对应点为P),使得点P、Q正好都在坐标轴上,求点P,Q的坐标;
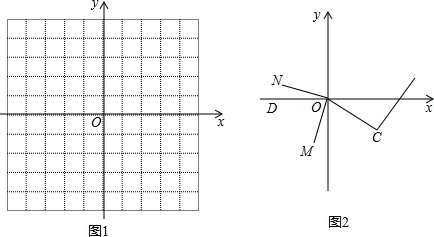
(3)点C(3,c),c≠0,D是x轴负半轴上任一点,连接OC,OM平分∠DOC,ON⊥OM,(ON在x轴上方),CE⊥CO,交x轴正半轴于点E,当c的值发生变化时,探究∠NOD与∠OEC之间的数量关系,并说明理由.
分析 (1)由非负数的性质即可求出a,b的值;
(2)根据平移的性质与坐标轴上点的坐标特征,分两种情况进行讨论:①P在y轴上,Q在x轴上;②P在x轴上,Q在y轴上;
(3)由角平分线定义可设∠DOM=∠MOC=α,根据垂直的定义得出∠NOD=90°-α,由平角的定义求出∠EOC=180°-2α,根据直角三角形两锐角互余得到∠OEC=90°-∠EOC=2α-90°,于是得出2∠NOD+∠OEC=90°.
解答 解:(1)∵$\sqrt{a-3}$+$\sqrt{-(4-b)^{2}}$=0,
∴a-3=0,4-b=0,
∴a=3,b=4;
(2)∵a=3,b=4,
∴A(1,3)、B(4,1),
∵x轴上点的纵坐标为0,y轴上点的横坐标为0,
∴如果平移线段AB至线段PQ处(A的对应点为P),使得点P、Q正好都在坐标轴上,可分两种情况:
①P在y轴上,Q在x轴上, 将线段AB先向左平移1个单位,再向下平移1个单位,此时P(0,2),Q(3,0);
将线段AB先向左平移1个单位,再向下平移1个单位,此时P(0,2),Q(3,0);
②P在x轴上,Q在y轴上,
将线段AB先向下平移3个单位,再向左平移4个单位,此时P(-3,0),Q(0,-2);
(3)2∠NOD+∠OEC=90°.理由如下:
∵OM平分∠DOC,
∴∠DOM=∠MOC,设∠DOM=∠MOC=α.
∵ON⊥OM,
∴∠NOD=90°-α,
∴∠EOC=180°-2α,
∵CE⊥CO,
∴∠OCE=90°,
∴∠OEC=90°-∠EOC=90°-(180°-2α)=2α-90°,
∴2∠NOD+∠OEC=2(90°-α)+(2α-90°)=90°.
点评 本题考查了作图-平移变换,非负数的性质,平移的性质,坐标轴上点的坐标特征,角平分线、垂直、平角的定义,直角三角形的性质,利用数形结合及分类讨论是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.在数-3,0,2,π四个数中,最大的是( )
| A. | -3 | B. | 0 | C. | 2 | D. | π |
14.8a3bm÷(28anb2)=$\frac{2}{7}$b2,则m,n的值为( )
| A. | m=2,n=3 | B. | m=1,n=3 | C. | m=4,n=3 | D. | m=4,n=1 |
15.在上午9时到10时之间,时钟的分针与时针会重合一次,这次的重合时间是( )
| A. | 9:48-9:49 | B. | 9:49-9:50 | C. | 9:50-9:51 | D. | 9:51-9:52 |
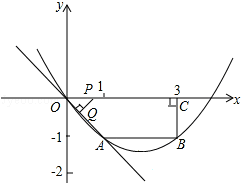 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动.过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.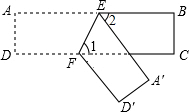 如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应.若∠1=65°,则∠2=50°.
如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应.若∠1=65°,则∠2=50°.