题目内容
2.已知函数y=$\frac{k}{x}$的图象经过点(-1,2),则y=kx的图象( )| A. | 在一、三象限 | B. | 在一、二象限 | C. | 在二、三象限 | D. | 在二、四象限 |
分析 根据反比例函数图象上点的坐标特点可得k=-1×2=-2,再根据正比例函数的性质可得答案.
解答 解:∵函数y=$\frac{k}{x}$的图象经过点(-1,2),
∴k=-1×2=-2,
∴y=kx的函数关系式为y=-2x,
∵k<0,
∴图象在第一、三象限.
故选:A.
点评 此题主要考查了反比例函数图象上点的坐标特点,以及正比例函数的性质,关键是掌握正比例函数y=kx,k>0,y随x的增大而增大,图象在第一三象限.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在数-3,0,2,π四个数中,最大的是( )
| A. | -3 | B. | 0 | C. | 2 | D. | π |
7.如果x2-6x+k是完全平方式,则k的值为( )
| A. | ±9 | B. | ±36 | C. | 36 | D. | 9 |
14.8a3bm÷(28anb2)=$\frac{2}{7}$b2,则m,n的值为( )
| A. | m=2,n=3 | B. | m=1,n=3 | C. | m=4,n=3 | D. | m=4,n=1 |
11.已知x1、x2是方程x2+3x-1=0的两根,则( )
| A. | x1+x2=-3,x1•x2=-1 | B. | x1+x2=-3,x1•x2=1 | ||
| C. | x1+x2=3,x1•x2=-1 | D. | x1+x2=3,x1•x2=1 |
12.一个三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
| A. | 24cm | B. | 21cm | C. | 13cm | D. | 9cm |
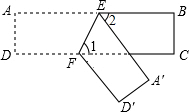 如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应.若∠1=65°,则∠2=50°.
如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应.若∠1=65°,则∠2=50°.