题目内容
13.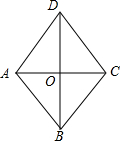 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 首先根据菱形的性质知AC垂直平分BD,再根据AC=AB知△ABC是正三角形,据此即可求出BD的长.
解答 解:∵四边形ABCD菱形,
∴AC⊥BD,
∵AC=AB=2,
∴△ABC是正三角形,
∴∠BAD=120°,
∴BO=sin60°•AC=$\sqrt{3}$,
∴BD=2$\sqrt{3}$.
故选:C.
点评 本题主要考查解直角三角形和菱形的性质的知识点,解答本题的关键是掌握菱形的对角线垂直平分.

练习册系列答案
相关题目
4.下列运算中正确的是( )
| A. | a•a2=a2 | B. | (a3)4=a7 | C. | (a2b)2=a4b2 | D. | 3x2•5x3=15x6 |
1.已知x=2是方程x2+bx-2=0的一个根,则b的值是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
18.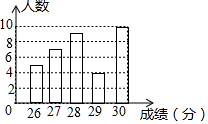 如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
 如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )| A. | 28分,30分 | B. | 28.5分,30分 | C. | 27.5分,28分 | D. | 28.2分,30分 |
5.地球绕太阳每小时转动通过的路程约是1.1×105千米,用科学记数法表示地球一天(以24小时计)转动通过的路程约是( )
| A. | 0.264×107千米 | B. | 2.64×106千米 | C. | 26.4×105千米 | D. | 264×104千米 |
15.与分式$\frac{-a+b}{-a-b}$相等的是( )
| A. | $\frac{a-b}{a+b}$ | B. | $-\frac{a+b}{a-b}$ | C. | $\frac{a+b}{a-b}$ | D. | $-\frac{a-b}{a+b}$ |
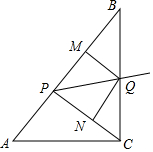 如图,已知在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,ON⊥CP于N.
如图,已知在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,ON⊥CP于N.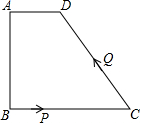 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)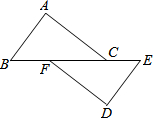 已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.
已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.