题目内容
7.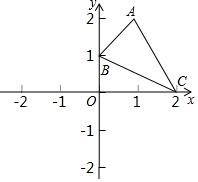 如图,在平面直角坐标系xOy中,A(1,2),B(0,1),C(2,0)若将△ABC平移到△A1B1C1,使点A1与原点重合,则点C1的坐标和△A1B1C1的面积分别是( )
如图,在平面直角坐标系xOy中,A(1,2),B(0,1),C(2,0)若将△ABC平移到△A1B1C1,使点A1与原点重合,则点C1的坐标和△A1B1C1的面积分别是( )| A. | C1(0,1),2 | B. | C1(0,1),1.5 | C. | C1(1,-2),2 | D. | C1(1,-2),1.5 |
分析 利用点A的平移规律得到三角形的平移规律,然后利用点平移的坐标特征写出C1点的坐标,然后计算出△ABC的面积得到△A1B1C1的面积.
解答 解:∵点A1与原点重合,
即点A(1,2)平移后原点,
∴△ABC先向左平移1和单位,再向下平移2个单位得到△A1B1C1,
∴点C1的坐标为(1,-2),
∵△ABC的面积=$\frac{1}{2}$(1+2)×2-$\frac{1}{2}$×1×2=2,
∴△A1B1C1的面积为2.
故选C.
点评 本题考查了坐标与图形变化-平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若a-b=8,a2-b2=72,则a+b的值为( )
| A. | 9 | B. | -9 | C. | 27 | D. | -27 |
2.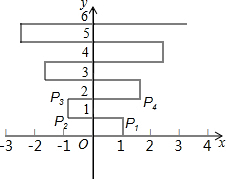 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
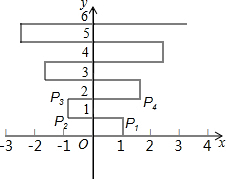 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )| A. | (504,1007) | B. | (505,1009) | C. | (1008,1007) | D. | (1009,1009) |
12.估算$\sqrt{21}$-2的值( )
| A. | 在1到2之间 | B. | 在2到3之间 | C. | 在3到4之间 | D. | 在4到5之间 |

 如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥BD?
如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度时,才能使AB′∥BD?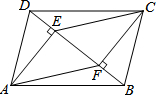 如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:
如图,在?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证: 已知点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
已知点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.