题目内容
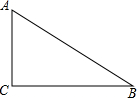 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
考点:作图—复杂作图,直线与圆的位置关系
专题:作图题
分析:(1)根据角平分线的作法求出角平分线BO;
(2)过O作OD⊥AB交AB于点D,先根据角平分线的性质求出DO=CO,再根据切线的判定定理即可得出答案.
(2)过O作OD⊥AB交AB于点D,先根据角平分线的性质求出DO=CO,再根据切线的判定定理即可得出答案.
解答:解:(1)如图:

(2)AB与⊙O相切.
证明:作OD⊥AB于D,如图.

∵BO平分∠ABC,∠ACB=90°,OD⊥AB,
∴OD=OC,
∴AB与⊙O相切.

(2)AB与⊙O相切.
证明:作OD⊥AB于D,如图.

∵BO平分∠ABC,∠ACB=90°,OD⊥AB,
∴OD=OC,
∴AB与⊙O相切.
点评:此题主要考查了复杂作图以及切线的判定等知识,正确把握切线的判定定理是解题关键.

练习册系列答案
相关题目
 已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.
已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.
 如图,在矩形AOCD中,把点D沿AE对折,使点D落在OC上的F点,已知AO=8.AD=10.
如图,在矩形AOCD中,把点D沿AE对折,使点D落在OC上的F点,已知AO=8.AD=10.
 如图,直线y=k1x+b与双曲线y=
如图,直线y=k1x+b与双曲线y= 如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=
如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=