Ő‚ńŅńŕ»›
 »ÁÕľ£¨‘ŕĺō–őAOCD÷–£¨į—Ķ„D—ōAE∂‘’Ř£¨ ĻĶ„D¬š‘ŕOC…ŌĶńFĶ„£¨“—÷™AO=8£ģAD=10£ģ
»ÁÕľ£¨‘ŕĺō–őAOCD÷–£¨į—Ķ„D—ōAE∂‘’Ř£¨ ĻĶ„D¬š‘ŕOC…ŌĶńFĶ„£¨“—÷™AO=8£ģAD=10£ģ£®1£©«ůFĶ„Ķń◊ÝĪÍ£Ľ
£®2£©»ÁĻŻ“ĽŐű≤Ľ”ŽŇ◊őÔŌŖ∂‘≥∆÷Š∆Ĺ––Ķń÷ĪŌŖ”Žł√Ň◊őÔŌŖĹŲ”–“ĽłŲĹĽĶ„£¨ő“√«į—’‚Őű÷ĪŌŖ≥∆ő™Ň◊őÔŌŖĶń«–ŌŖ£¨“—÷™Ň◊őÔŌŖĻżĶ„O£¨F£¨«“÷ĪŌŖy=6x-36 «ł√Ň◊őÔŌŖĶń«–ŌŖ£¨«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®3£©÷ĪŌŖy=k£®x-3£©-
| 35 |
| 4 |
| 35 |
| 4 |
| 1 |
| PB |
| 1 |
| QB |
| (x2-x1)2+(y2-y1)2 |
ŅľĶ„£ļ∂ĢīőļĮ ż◊ŘļŌŐ‚,ŃĹĶ„ľšĶńĺŗņŽ
◊®Ő‚£ļ—Ļ÷ŠŐ‚
∑÷őŲ£ļ£®1£©łýĺ›’ŘĶĢĶń–‘÷ Ķ√ĶĹAF=AD£¨ňý“‘‘ŕ‘ŕ÷ĪĹ«°ųAOF÷–£¨ņŻ”√ĻīĻ…∂®ņŪņī«ůOFĶń≥§∂»£¨»Ľļů”…Ķ„F‘ŕx÷Š…Ō“◊«ůĶ„FĶń◊ÝĪÍ£Ľ
£®2£©“—÷™Ň◊őÔŌŖ”Žx÷ŠĶńŃĹłŲĹĽĶ„◊ÝĪÍ£¨ňý“‘Ņ…“‘…ŤŇ◊őÔŌŖĶńĹĽĶ„ Ĺ∑Ĺ≥Őy=a£®x-0£©£®x-6£©£¨ľīy=ax£®x-6£©£®a°Ŕ0£©£ģłýĺ›Ň◊őÔŌŖĶń«–ŌŖĶń∂®“Ś÷™£¨÷ĪŌŖy=6x-36”Žł√Ň◊őÔŌŖ”–“ĽłŲĹĽĶ„£¨‘ÚŃ™ŃĘŃĹłŲļĮ żĹ‚őŲ Ĺ£¨Ķ√ĶĹĻō”ŕxĶń“Ľ‘™∂Ģīő∑Ĺ≥Őax2-£®6a+6£©x+36=0£¨‘Úł√∑Ĺ≥ŐĶńłýĶńŇ–Īū Ĺ°ų=0£Ľ
£®3£©…ŤP£®x1£¨y1£©£¨Q£®x2£¨y2£©£¨ľŔ…Ťx1£ĺ3£¨x2£ľ3£ģłýĺ›Ň◊őÔŌŖ”Ž÷ĪŌŖĶńĹĽĶ„◊ÝĪÍĶń«ů∑®Ķ√ĶĹ£ļx2-(6+k)x+3k+
=0£¨łý図ý”ŽŌĶ żĶńĻōŌĶ«ůĶ√x1+x2=6+k£¨x1•x2=3k+
£ģņŻ”√ŃĹĶ„ľšĶńĺŗņŽĻę ĹÕ∆÷™
+
=
•
£¨“◊«ů
•
=
ő™∂®÷Ķ£ģ
£®2£©“—÷™Ň◊őÔŌŖ”Žx÷ŠĶńŃĹłŲĹĽĶ„◊ÝĪÍ£¨ňý“‘Ņ…“‘…ŤŇ◊őÔŌŖĶńĹĽĶ„ Ĺ∑Ĺ≥Őy=a£®x-0£©£®x-6£©£¨ľīy=ax£®x-6£©£®a°Ŕ0£©£ģłýĺ›Ň◊őÔŌŖĶń«–ŌŖĶń∂®“Ś÷™£¨÷ĪŌŖy=6x-36”Žł√Ň◊őÔŌŖ”–“ĽłŲĹĽĶ„£¨‘ÚŃ™ŃĘŃĹłŲļĮ żĹ‚őŲ Ĺ£¨Ķ√ĶĹĻō”ŕxĶń“Ľ‘™∂Ģīő∑Ĺ≥Őax2-£®6a+6£©x+36=0£¨‘Úł√∑Ĺ≥ŐĶńłýĶńŇ–Īū Ĺ°ų=0£Ľ
£®3£©…ŤP£®x1£¨y1£©£¨Q£®x2£¨y2£©£¨ľŔ…Ťx1£ĺ3£¨x2£ľ3£ģłýĺ›Ň◊őÔŌŖ”Ž÷ĪŌŖĶńĹĽĶ„◊ÝĪÍĶń«ů∑®Ķ√ĶĹ£ļx2-(6+k)x+3k+
| 35 |
| 4 |
| 35 |
| 4 |
| 1 |
| PB |
| 1 |
| QB |
| 1 | ||
|
| ||
| 3(x1+x2)-x1x2-9 |
| 1 | ||
|
| ||
9-
|
| 4 |
| 73 |
Ĺ‚īū£ļĹ‚£ļ£®1£©”…’ŘĶĢĶń–‘÷ Ķ√ĶĹ£ļ°ųADE°’°ųAFE£¨‘ÚAF=AD£ģ
”÷°ŖAD=10£¨AO=8£¨
°ŗOF=
=
=6£¨
°ŗF£®6£¨0£©£Ľ
 £®2£©“ņŐ‚“‚Ņ……ŤĻżĶ„O°ĘFĶńŇ◊őÔŌŖĹ‚őŲ Ĺő™y=a£®x-0£©£®x-6£©£¨ľīy=ax£®x-6£©£®a°Ŕ0£©£ģ
£®2£©“ņŐ‚“‚Ņ……ŤĻżĶ„O°ĘFĶńŇ◊őÔŌŖĹ‚őŲ Ĺő™y=a£®x-0£©£®x-6£©£¨ľīy=ax£®x-6£©£®a°Ŕ0£©£ģ
“ņŐ‚“‚÷™£¨Ň◊őÔŌŖ”Ž÷ĪŌŖy=6x-36Ōŗ«–£¨
°ŗ
£¨
°ŗax2-£®6a+6£©x+36=0 ”–ŃĹłŲŌŗĶ»Ķń Ķ żłý£¨
°ŗ°ų=[-£®6a+6£©]2-4a°Ń36=0£¨
Ĺ‚Ķ√a=1£¨
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™ y=x2-6x£Ľ
£®3£©÷§√ų£ļ…ŤP£®x1£¨y1£©£¨Q£®x2£¨y2£©£¨ľŔ…Ťx1£ĺ3£¨x2£ľ3£ģ
“ņŐ‚“‚Ķ√
£¨
Ķ√ x2-(6+k)x+3k+
=0£¨
°ŗx1+x2=6+k£¨x1•x2=3k+
£ģ
°Ŗ
+
=
+
=
+
=
(
+
)
=
•
=
•
ľī
•
=4ő™∂®÷Ķ£ģ
”÷°ŖAD=10£¨AO=8£¨
°ŗOF=
| AF2-OA2 |
| 102-82 |
°ŗF£®6£¨0£©£Ľ
 £®2£©“ņŐ‚“‚Ņ……ŤĻżĶ„O°ĘFĶńŇ◊őÔŌŖĹ‚őŲ Ĺő™y=a£®x-0£©£®x-6£©£¨ľīy=ax£®x-6£©£®a°Ŕ0£©£ģ
£®2£©“ņŐ‚“‚Ņ……ŤĻżĶ„O°ĘFĶńŇ◊őÔŌŖĹ‚őŲ Ĺő™y=a£®x-0£©£®x-6£©£¨ľīy=ax£®x-6£©£®a°Ŕ0£©£ģ“ņŐ‚“‚÷™£¨Ň◊őÔŌŖ”Ž÷ĪŌŖy=6x-36Ōŗ«–£¨
°ŗ
|
°ŗax2-£®6a+6£©x+36=0 ”–ŃĹłŲŌŗĶ»Ķń Ķ żłý£¨
°ŗ°ų=[-£®6a+6£©]2-4a°Ń36=0£¨
Ĺ‚Ķ√a=1£¨
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™ y=x2-6x£Ľ
£®3£©÷§√ų£ļ…ŤP£®x1£¨y1£©£¨Q£®x2£¨y2£©£¨ľŔ…Ťx1£ĺ3£¨x2£ľ3£ģ
“ņŐ‚“‚Ķ√
|
Ķ√ x2-(6+k)x+3k+
| 35 |
| 4 |
°ŗx1+x2=6+k£¨x1•x2=3k+
| 35 |
| 4 |
°Ŗ
| 1 |
| PB |
| 1 |
| QB |
| 1 | ||||
|
| 1 | ||||
|
=
| 1 | ||
|
| 1 | ||
|
=
| 1 | ||
|
| 1 |
| x1-3 |
| 1 |
| 3-x2 |
=
| 1 | ||
|
| x1-x2 |
| 3(x1+x2)-x1x2-9 |
=
| 1 | ||
|
| ||
| 3(x1+x2)-x1x2-9 |
ľī
| 1 | ||
|
| ||
9-
|
Ķ„∆ņ£ļĪĺŐ‚÷ų“™Ņľ≤ťŃň∂ĢīőļĮ żĹ‚őŲ ĹĶń»∑∂®°ĘļĮ żÕľŌůĹĽĶ„Ķń«ů∑®Ķ»÷™ ∂Ķ„£ģĹ‚Ő‚ Ī£¨“™—ß…ķ’∆ő’ ż–őĹŠļŌĶń ż—ßňľŌŽ∑Ĺ∑®£ģŃŪÕ‚£¨Ĺ‚īū£®3£©Ő‚ Ī£¨–Ť“™ žŌ§ŃĹĶ„ľšĶńĺŗņŽĻę Ĺ£ģ

Ń∑Ōį≤ŠŌĶŃ–īūįł
ŌŗĻōŐ‚ńŅ
 »ÁÕľ£¨‘ŕ∆Ĺ––ňńĪŖ–őABCD÷–£¨AB=4£¨°ŌBADĶń∆Ĺ∑÷ŌŖ”ŽBCĶń—”≥§ŌŖĹĽ”ŕĶ„E£¨”ŽDCĹĽ”ŕĶ„F£¨«“Ķ„Fő™ĪŖDCĶń÷–Ķ„£¨DG°ÕAE£¨īĻ◊„ő™G£¨»ŰDG=1£¨«ůAEĶń≥§£ģ
»ÁÕľ£¨‘ŕ∆Ĺ––ňńĪŖ–őABCD÷–£¨AB=4£¨°ŌBADĶń∆Ĺ∑÷ŌŖ”ŽBCĶń—”≥§ŌŖĹĽ”ŕĶ„E£¨”ŽDCĹĽ”ŕĶ„F£¨«“Ķ„Fő™ĪŖDCĶń÷–Ķ„£¨DG°ÕAE£¨īĻ◊„ő™G£¨»ŰDG=1£¨«ůAEĶń≥§£ģ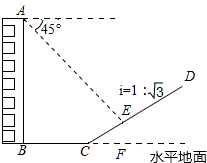 »ÁÕľ£¨“Ľ¬•∑ŅABļů”–“ĽľŔ…Ĺ£¨∆š∆¬∂»ő™i=1£ļ
»ÁÕľ£¨“Ľ¬•∑ŅABļů”–“ĽľŔ…Ĺ£¨∆š∆¬∂»ő™i=1£ļ »ÁÕľ£¨‘ŕRt°ųABC÷–£¨°ŌACB=90°„£ģ
»ÁÕľ£¨‘ŕRt°ųABC÷–£¨°ŌACB=90°„£ģ