题目内容
 已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.
已知:如图,在△ABC中,AB=AC,D为BC上的一点,DA平分∠EDC,且∠E=∠B.求证:△ADE≌△ADC.考点:全等三角形的判定
专题:证明题
分析:首先由角平分线的性质得出∠ADE=∠ADC,再由等腰三角形的性质结合∠E=∠B,可得∠E=∠C,运用AAS定理可进行全等的证明.
解答:证明:∵DA平分∠EDC,
∴∠ADE=∠ADC,
∵AB=AC,
∴∠B=∠C,
又∵∠E=∠B,
∴∠E=∠C,
在△ADE和△ADC中,
,
∴△ADE≌△ADC(AAS).
∴∠ADE=∠ADC,
∵AB=AC,
∴∠B=∠C,
又∵∠E=∠B,
∴∠E=∠C,
在△ADE和△ADC中,
|
∴△ADE≌△ADC(AAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
上海世博会的中国馆利用太阳能发电,年发电量可达2 840 000度,2 840 000用科学记数法可表示为( )
| A、2.84×107 |
| B、2.84×106 |
| C、2.84×105 |
| D、28.4×106 |
 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示
如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
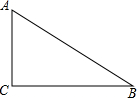 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.