题目内容
在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
考点:解直角三角形
专题:压轴题,分类讨论
分析:根据题意画出图形,分4种情况进行讨论,利用直角三角形的性质解答.
解答:解:如图1:

当∠C=60°时,∠ABC=30°,与∠ABP=30°矛盾;
如图2:

当∠C=60°时,∠ABC=30°,
∵∠ABP=30°,
∴∠CBP=60°,
∴△PBC是等边三角形,
∴CP=BC=6;
如图3:

当∠ABC=60°时,∠C=30°,
∵∠ABP=30°,
∴∠PBC=60°-30°=30°,
∴PC=PB,
∵BC=6,
∴AB=3,
∴PC=PB=
=
=2
;
如图4:

当∠ABC=60°时,∠C=30°,
∵∠ABP=30°,
∴∠PBC=60°+30°=90°,
∴PC=BC÷cos30°=4
.
故答案为:6或2
或4
.

当∠C=60°时,∠ABC=30°,与∠ABP=30°矛盾;
如图2:

当∠C=60°时,∠ABC=30°,
∵∠ABP=30°,
∴∠CBP=60°,
∴△PBC是等边三角形,
∴CP=BC=6;
如图3:

当∠ABC=60°时,∠C=30°,
∵∠ABP=30°,
∴∠PBC=60°-30°=30°,
∴PC=PB,
∵BC=6,
∴AB=3,
∴PC=PB=
| 3 |
| cos30° |
| 3 | ||||
|
| 3 |
如图4:

当∠ABC=60°时,∠C=30°,
∵∠ABP=30°,
∴∠PBC=60°+30°=90°,
∴PC=BC÷cos30°=4
| 3 |
故答案为:6或2
| 3 |
| 3 |
点评:本题考查了解直角三角形,熟悉特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
给出下列图形名称:(1)线段;(2)直角;(3)等腰三角形;(4)平行四边形;(5)长方形,在这五种图形中是轴对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
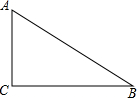 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.