题目内容
20. 以菱形ABCD的对角线交点O为坐标原点,AC所在的直线为x轴,已知A(-4,0),B(0,-2),M(0,4),P为折线BCD上一动点,作PE⊥y轴于点E,设点P的纵坐标为a.
以菱形ABCD的对角线交点O为坐标原点,AC所在的直线为x轴,已知A(-4,0),B(0,-2),M(0,4),P为折线BCD上一动点,作PE⊥y轴于点E,设点P的纵坐标为a.(1)求BC边所在直线的解析式;
(2)设y=MP2+OP2,求y关于a的函数关系式;
(3)当△OPM为直角三角形时,求点P的坐标.
分析 (1)先确定出OA=4,OB=2,再利用菱形的性质得出OC=4,OD=2,最后用待定系数法即可确定出直线BC解析式;
(2)分两种情况,先表示出点P的坐标,利用两点间的距离公式即可得出函数关系式;
(3)分两种情况,利用勾股定理的逆定理建立方程即可求出点P的坐标.
解答 解:(1)∵A(-4,0),B(0,-2),
∴OA=4,OB=2,
∵四边形ABCD是菱形,
∴OC=OA=4,OD=OB=2,
∴C(4,0),D(0,2),
设直线BC的解析式为y=kx-2,
∴4k-2=0,
∴k=$\frac{1}{2}$,
∴直线BC的解析式为y=$\frac{1}{2}$x-2;
(2)由(1)知,C(4,0),D(0,2),
∴直线CD的解析式为y=-$\frac{1}{2}$x+2,
由(1)知,直线BC的解析式为y=$\frac{1}{2}$x-2,
当点P在边BC上时,
设P(2a+4,a)(-2≤a<0),
∵M(0,4),
∴y=MP2+OP2=(2a+4)2+(a-4)2+(2a+4)2+a2=2(2a+4)2+(a-4)2+a2=10a2+24a+48
当点P在边CD上时,
∵点P的纵坐标为a,
∴P(4-2a,a)(0≤a≤2),
∵M(0,4),
∴y=MP2+OP2=(4-2a)2+(a-4)2+(4-2a)2+a2=10a2-40a+48,
(3)①当点P在边BC上时,即:0≤a≤2,
由(2)知,P(2a+4,a),
∵M(0,4),
∴OP2=(2a+4)2+a2=5a2+16a+16,PM2=(2a+4)2+(a-4)2=5a2-8a+32,OM2=16,
∵△POM是直角三角形,易知,PM最大,
∴OP2+OM2=PM2,
∴5a2+16a+16+16=5a2-8a+32,
∴a=0(舍)
②当点P在边CD上时,即:0≤a≤2时,
由(2)知,P(4-2a,a),
∵M(0,4),
∴OP2=(4-2a)2+a2=5a2-16a+16,PM2=(4-2a)2+(a-4)2=5a2-24a+32,OM2=16,
∵△POM是直角三角形,
Ⅰ、当∠POM=90°时,
∴OP2+OM2=PM2,
∴5a2-16a+16+16=5a2-24a+32,
∴a=0,
∴P(4,0),
Ⅱ、当∠MPO=90°时,OP2+PM2=5a2-16a+16+5a2-24a+32=10a2-40a+48=OM2=16,
∴a=2+$\frac{2\sqrt{5}}{5}$(舍)或a=2-$\frac{2\sqrt{5}}{5}$,
∴P($\frac{4\sqrt{5}}{5}$,2-$\frac{2\sqrt{5}}{5}$),
即:当△OPM为直角三角形时,点P的坐标为($\frac{4\sqrt{5}}{5}$,2-$\frac{2\sqrt{5}}{5}$),(4,0).
点评 此题是四边形综合题,主要考查了菱形的性质,勾股定理逆定理,两点间的距离公式,待定系数法,解(1)的关键是掌握待定系数法,解(2)的关键是分类讨论的思想,解(3)的关键是分两种情况,利用勾股定理逆定理建立方程求解,是一道中等难度的题目.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案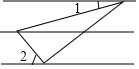 如图,小明把一块含有60°锐角的直角三角板的三个顶点分别放在一组平行线上,如果∠1=20°,那么∠2的度数是( )
如图,小明把一块含有60°锐角的直角三角板的三个顶点分别放在一组平行线上,如果∠1=20°,那么∠2的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 45° |

| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
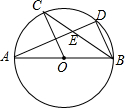 如图,AB是⊙O的直径,C,D是⊙O上的点(C,D在AB的同侧),且OC∥BD,连结AD,与BC,OC分别交于点E,F,则不一定成立的是( )
如图,AB是⊙O的直径,C,D是⊙O上的点(C,D在AB的同侧),且OC∥BD,连结AD,与BC,OC分别交于点E,F,则不一定成立的是( )| A. | AD⊥BD | B. | CB平分∠ABD | C. | BD=2OF | D. | △CEF≌△BED |
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{48}$÷$\sqrt{3}$=4 | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{4}$=±2 |
| A. | -7 | B. | -$\frac{4}{7}$ | C. | $\frac{1}{7}$ | D. | 7 |
 如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )
如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使b∥a,其画法的依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 两直线平行,同位角相等 | |
| C. | 过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 内错角相等,两直线平行 |
 如图,已知AB是⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD=25°.
如图,已知AB是⊙O的直径,CD是⊙O的弦,∠ABD=65°,则∠BCD=25°. 已知:如图,直线a⊥m,直线b⊥m,若∠1=60°,则∠2的度数是120°.
已知:如图,直线a⊥m,直线b⊥m,若∠1=60°,则∠2的度数是120°.