题目内容
 如图,菱形ABCD,对角线AC与BD相交于O,AB=5,AO=4,菱形面积为
如图,菱形ABCD,对角线AC与BD相交于O,AB=5,AO=4,菱形面积为考点:菱形的性质
专题:
分析:根据菱形的性质可得AC⊥BD,然后利用勾股定理求出OB的值,最后根据菱形的面积公式求解.
解答:解:∵四边形ABCD为菱形,
∴AC⊥BD,
则OB=
=3,
∴AC=8,BD=6,
S菱形ABCD=
AC•BD=
×6×8=24.
故答案为:24.
∴AC⊥BD,
则OB=
| AB2-AO2 |
∴AC=8,BD=6,
S菱形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:24.
点评:本题考查了菱形的性质,解答本题的关键是掌握菱形的两条对角线互相垂直的性质.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为( )
如图,函数y=kx(k≠0)和y=ax+4(a≠0)的图象相交于点A(2,3),则不等式kx>ax+4的解集为( )| A、x>3 | B、x<3 |
| C、x>2 | D、x<2 |
无论x取何值时,下列分式中总有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中,是一次函数但不是正比例函数的为( )
A、y=-
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
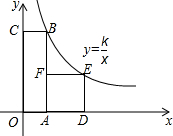 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=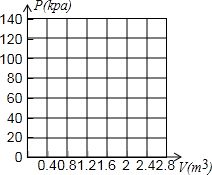 在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表:
在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表: