题目内容
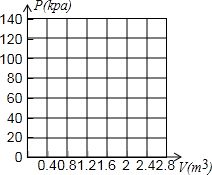 在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表:
在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表:| V(m3) | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 |
| p(kpa) | 120 | 80 | 60 | 48 | 40 |
(2)确定p与V的函数关系式,并在如图的坐标系内画出该函数的大致图象;
(3)当气球内的气体压强大于140kpa时,气球将爆炸,为了安全起见,气体的体积V(m3)的取值范围是
考点:反比例函数的应用
专题:
分析:(1)根据p与v的乘积是定值可以确定两变量之间的函数关系;
(2)利用待定系数法确定反比例函数的解析式即可;
(3)代入p≥140确定v的取值范围即可.
(2)利用待定系数法确定反比例函数的解析式即可;
(3)代入p≥140确定v的取值范围即可.
解答:解:(1)②;
(2)设P=
,将V=1.2,P=80代入,得 m=1.2×80=96.
∴P与V的关系式为P=
;
图象为:

(3)当P=
≥140时,
解得:V≥
,
故答案为:V≥
.
(2)设P=
| m |
| v |
∴P与V的关系式为P=
| 96 |
| v |
图象为:

(3)当P=
| 96 |
| v |
解得:V≥
| 24 |
| 35 |
故答案为:V≥
| 24 |
| 35 |
点评:本题考查了反比例函数的应用,解题的关键是发现两变量之间的关系并确定反比例函数的解析式.

练习册系列答案
相关题目
 如图,菱形ABCD,对角线AC与BD相交于O,AB=5,AO=4,菱形面积为
如图,菱形ABCD,对角线AC与BD相交于O,AB=5,AO=4,菱形面积为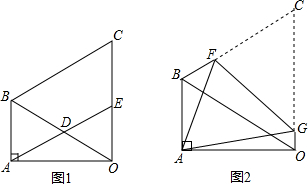 如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E. 如图,线段BC切⊙O于点C,以AC为直径,连接AB交⊙O于点D,点E是BC的中点,交AB于点D,连结OB、DE交于点F.
如图,线段BC切⊙O于点C,以AC为直径,连接AB交⊙O于点D,点E是BC的中点,交AB于点D,连结OB、DE交于点F.