题目内容
在平行四边形ABCD中,∠B-∠A=20°,则∠D的度数是 .
考点:平行四边形的性质
专题:
分析:根据平行四边形的基本性质可知,平行四边形的邻角互补,由已知可得,∠A、∠B是邻角,故∠B可求解;然后由“平行四边形的对角相等”的性质得到∠D=∠B.
解答: 解:∵在平行四边形ABCD中,∠B+∠A=180°,∠B-∠A=20°,
解:∵在平行四边形ABCD中,∠B+∠A=180°,∠B-∠A=20°,
∴2∠B=200°,
∴∠B=100°.
又∵∠D=∠B,
∴∠D=100°.
故答案为:100°.
 解:∵在平行四边形ABCD中,∠B+∠A=180°,∠B-∠A=20°,
解:∵在平行四边形ABCD中,∠B+∠A=180°,∠B-∠A=20°,∴2∠B=200°,
∴∠B=100°.
又∵∠D=∠B,
∴∠D=100°.
故答案为:100°.
点评:本题考查了平行四边形的性质.掌握平行四边形的相邻内角互为补角,相对内角相等是解答本题的关键,属于基础题,比较简单.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
(-ab)(-ab)(-ab)的积是正数,则( )
| A、ab>0 |
| B、ab<0 |
| C、a>0,b<0 |
| D、a<0,b>0 |
 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,求证:AE=EF+BF.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,求证:AE=EF+BF.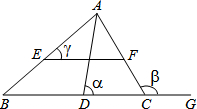 如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则:
如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则: 如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF,
如图,F在BD上,BC、AD相交于点E,且AB∥CD∥EF, 如图,菱形ABCD,对角线AC与BD相交于O,AB=5,AO=4,菱形面积为
如图,菱形ABCD,对角线AC与BD相交于O,AB=5,AO=4,菱形面积为