题目内容
4.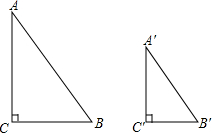 已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.求证:Rt△ABC∽Rt△A′B′C′.
分析 在AC上截取AD=A′C′,在AB上截取AE=A′B′,连接DE,先证明△ABC∽△AED,得出∠ADE=∠C=90°,再由HL证明Rt△AED≌Rt△A′B′C′,即可得出结论.
解答 证明:在AC上截取AD=A′C′,在AB上截取AE=A′B′,连接DE,如图所示: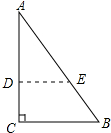
∵$\frac{AB}{A′B′}=\frac{AC}{A′C′}$,
∴$\frac{AB}{AD}=\frac{AC}{AE}$,
又∵∠A=∠A,
∴△ABC∽△AED,
∴∠ADE=∠C=90°,∠C=∠C′=90°,
∴∠ADE=∠C′=90°,
在Rt△AED和Rt△A′B′C′中,$\left\{\begin{array}{l}{AE=A′B′}\\{AD=A′C′}\end{array}\right.$,
∴Rt△AED≌Rt△A′B′C′(HL),
∴Rt△ABC∽Rt△A′B′C′.
点评 本题考查了相似三角形的判定、全等三角形的判定;熟练掌握相似三角形的判定方法,通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,∠A=80°,D,E,F分别是BC,AB,AC边上的点,且BD=BE,CD=CF,求∠EDF的度数.
如图,在△ABC中,∠A=80°,D,E,F分别是BC,AB,AC边上的点,且BD=BE,CD=CF,求∠EDF的度数.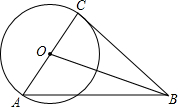 如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.
如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.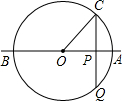 如图,直线AB经过⊙O的圆心,且与⊙O相交于A,B两点,点C在⊙0上,且∠AOC是锐角.点P是直线AB上一个动点(不与点O重合),直线PC与⊙O相交于点Q,是否存在点P.使得QP=QO?如果存在,这样的点P共有几个?如果不存在,请说明理由.
如图,直线AB经过⊙O的圆心,且与⊙O相交于A,B两点,点C在⊙0上,且∠AOC是锐角.点P是直线AB上一个动点(不与点O重合),直线PC与⊙O相交于点Q,是否存在点P.使得QP=QO?如果存在,这样的点P共有几个?如果不存在,请说明理由. 如图,已知⊙A、⊙B和⊙C两两相切,已知AB=6cm,BC=5cm,AC=4cm,求这三个圆的半径.
如图,已知⊙A、⊙B和⊙C两两相切,已知AB=6cm,BC=5cm,AC=4cm,求这三个圆的半径.