题目内容
19．
数a，b在数轴上对应的点如图所示，试化简|a+b|+|b-a|+|b|．
分析 根据数轴判断a+b、b-a、b与0的大小关系，再利用绝对值的性质化简．
解答 解：由数轴可知：a＜0＜b，a+b＜0，b-a＞0，
∴原式=-（a+b）+（b-a）+b=-2a+b；
点评 本题考查数轴，涉及有理数大小比较，绝对值的性质等知识，属于基础题型．
练习册系列答案
相关题目
算筹是我国古代的计算工具之一，也是中华民族智慧的结晶，如图1中用算筹表示的算式是“7408+2366”，则图2中算筹表示的算式的运算结果为-426．
10．问题背景：表是某通讯公司推出的移动电话两种计费方式：
若设一个月内用移动电话主叫为t分（t为正整数），根据主叫时间t分析并选择省钱的计费方式．
分析说明：由上表可知，计费与主叫时间相关，计费时首先要看主叫是否超过限定时间．因此，考虑t的取值时，两个主叫限定时间150分和350分是不同时间范围的划分点．
列表解析：当t在不同时间范围内取值时，方式一和方式二的计费如表：（用含t的代数式将表填写完整）
探索比较：由以上分析可知，计费随着主叫时间的变化而变化，比较如下：
①当t小于或等于150分时，因为58＜88，所以按方式一的计费少；
②当t大于150且小于350时，方式一的计费由58元增加到108元，而方式二的计费一直是88元，故可能存在某主叫时间按方式一和方式二的计费相等，请你列方程给予解答说明．
③当t=350时，因为108＞88，所以按方式二的计费较少；
④当t大于350时，由上表可以看出，方式一的计费为108元加上超过350分部分的超时费，方式二的计费为88元加上超过350分部分的超时费，所以按方式二的计费少．
归纳发现：综合上述分析，可以发现：
主叫时间小于270分时，选择方式一省钱；
主叫时间大于270分时，选择方式二省钱．
| 月使用费/元 | 主叫限定时间/分 | 主叫超时费/（元/分） | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
分析说明：由上表可知，计费与主叫时间相关，计费时首先要看主叫是否超过限定时间．因此，考虑t的取值时，两个主叫限定时间150分和350分是不同时间范围的划分点．
列表解析：当t在不同时间范围内取值时，方式一和方式二的计费如表：（用含t的代数式将表填写完整）
| 主叫时间t/分 | 方式一计费/元 | 方式二计费/元 |
| t小于150 | 58 | 88 |
| t=150 | 58 | 88 |
| t大于150且小于350 | 58+0.25（t-150） | 88 |
| t=350 | 108 | 88 |
| t大于350 | 108+0.25（t-350） | 88+0.19（t-350） |
①当t小于或等于150分时，因为58＜88，所以按方式一的计费少；
②当t大于150且小于350时，方式一的计费由58元增加到108元，而方式二的计费一直是88元，故可能存在某主叫时间按方式一和方式二的计费相等，请你列方程给予解答说明．
③当t=350时，因为108＞88，所以按方式二的计费较少；
④当t大于350时，由上表可以看出，方式一的计费为108元加上超过350分部分的超时费，方式二的计费为88元加上超过350分部分的超时费，所以按方式二的计费少．
归纳发现：综合上述分析，可以发现：
主叫时间小于270分时，选择方式一省钱；
主叫时间大于270分时，选择方式二省钱．
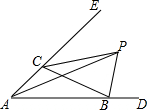如图，在△ABC中，点P是△ABC的外角∠DBC、∠BCE的平分线的交点，若∠BPC=72°，连接AP，则∠BAP=18 度．
已知，如图，△ABC是直角三角形，∠ACB=90°，∠ABC=60°，BC=6cm，点P由C开始向点B以1cm/s的速度运动，点Q由B开始向点A以2cm/s的速度运动，若PQ同时开始运动
在平面直角坐标系中，ABCD是正方形，且A（0，1）、B（2，0）．