题目内容
7.Rt△ABC中,∠C=90°,AC=3,BC=4,则内心I与重心G之间的距离IG=$\frac{1}{3}$.分析 构造如图所示的坐标系,从而可求得点M,N的坐标,然后求得直线CN与BM的解析式,从而可解得点G的坐标,然后三角形的内圆的性质求得点I的坐标,最后利用两点之间的距离公式可求得IG的长度.
解答 解:构造如图所示的平面直角坐标系.
∵BM、CN是三角形的中线,
∴点M的坐标的为(2,0),点N的坐标为(2,1.5).
∴直线CN的解析式为y=$\frac{4}{3}x$,直线MB的解析式为y=$-\frac{2}{3}x+2$.
将y=$\frac{4}{3}x$与y=$-\frac{2}{3}x+2$联立.
解得:x=1,y=$\frac{4}{3}$.
∵∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
设圆I的半径为r.则$\frac{1}{2}×(3+4+5)r$=$\frac{1}{2}×3×4$.
解得r=1.
∴点I的坐标为(1,1).
∴GI=$\frac{4}{3}-1$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查的是三角形的内心和重心,一次函数的解析式、解二元一次方程组,根据题意构造如图所示的坐标系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若A(-4,y1),B(-3,y2),C(3,y3)为二次函数y=x2+2x-6的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
19.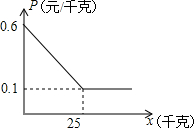 某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
(1)求出价格P(元/千克)与卖给餐厅的土豆数量x(千克)之间的关系式.
(2)设每天小贩从批发市场批发土豆的数量为x(千克),每月所得的毛利润为W(元).
①根据具体的x(千克)的值,填写下表:
②该小贩每天从批发市场买进多少千克土豆才能使每月所获得利润最大?最多可赚多少钱?
 某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.(1)求出价格P(元/千克)与卖给餐厅的土豆数量x(千克)之间的关系式.
(2)设每天小贩从批发市场批发土豆的数量为x(千克),每月所得的毛利润为W(元).
①根据具体的x(千克)的值,填写下表:
| 所批发土豆的数量x(千克) | 70 | 90 | 100 |
| 每月所得毛利润W(元) | 420 | 540 | 570 |
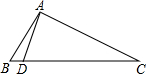 如图,在△ABC中,∠B=2∠C,点D在BC边上,且AD⊥AC,求证:CD=2AB.
如图,在△ABC中,∠B=2∠C,点D在BC边上,且AD⊥AC,求证:CD=2AB. 如图,平行四边形ABCD中,如果把图中线段都画成有向线段,那么在这些有向线段所表示的向量中,用符号把符合下列要求的向量表示出来:
如图,平行四边形ABCD中,如果把图中线段都画成有向线段,那么在这些有向线段所表示的向量中,用符号把符合下列要求的向量表示出来: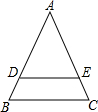 如图,在△ABC中,已知DE∥BC,AE=3EC,S△ABC=48,求S△ADE及S四边形BCED.
如图,在△ABC中,已知DE∥BC,AE=3EC,S△ABC=48,求S△ADE及S四边形BCED. 如图所示,在5×5的正方形网格中,有格点△ABC,请你在图中画出符合下列三个要求的最小△A1B1C1和最大△A2B2C2.
如图所示,在5×5的正方形网格中,有格点△ABC,请你在图中画出符合下列三个要求的最小△A1B1C1和最大△A2B2C2.