题目内容
12．
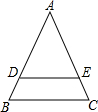如图，在△ABC中，已知DE∥BC，AE=3EC，S△ABC=48，求S△ADE及S四边形BCED．
分析 由DE∥BC，可得△ADE∽△ABC，然后根据相似三角形面积的比等于相似比的平方，可求得△ADE的面积，继而求得四边形BCED的面积．
解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∵AE=3EC，
∴AE：AC=3：4，
∴S△ADE：S△ABC=9：16，
∵S△ABC=48，
∴S△ADE=27，
∴S四边形BCED=S△ABC-S△ADE=48-27=21．
点评 此题考查了相似三角形的判定与性质．此题难度不大，注意掌握相似三角形面积的比等于相似比的平方定理的应用是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．
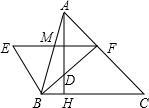如图，△ABC中，AH⊥BC，BF平分∠ABC，BE⊥BF，EF∥BC，以下四个结论：①∠E=∠ABE；②∠ADF-∠BAH=$\frac{1}{2}$∠ABC；③∠ADF=∠AFD；④S△ABF=$\frac{FM•AH}{2}$．其中正确的有（ ）
如图，△ABC中，AH⊥BC，BF平分∠ABC，BE⊥BF，EF∥BC，以下四个结论：①∠E=∠ABE；②∠ADF-∠BAH=$\frac{1}{2}$∠ABC；③∠ADF=∠AFD；④S△ABF=$\frac{FM•AH}{2}$．其中正确的有（ ）| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
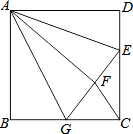如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF．下列结论：
如图所示，在公路MN的北侧有A、B两家工厂，现要在公路边建一仓库P，要求路程PA与PB的和最短，请用所学的知识确定点P的位置．