题目内容
如图，已知△AOB中，∠AOB=90°，OD⊥AB于点D．以点O为圆心，OD为半径的圆交OA于点E，在BA上截取BC=OB，求证：CE是⊙O的切线．考点：切线的判定
专题：证明题
分析：连接CO，然后根据余角的性质证明∠3=∠4，再证明△CEO≌△CDO可得∠CEO=∠CDO=90°，进而得到CE是⊙O的切线．
解答：
证明：连接CO，
∵BC=OB，
∴∠1=∠2，
∵∠AOB=90°，
∴∠2+∠4=90°，
∵OD⊥AB，
∴∠1+∠3=90°，
∴∠3=∠4，
在△CEO和△CDO中
，
∴△CEO≌△CDO（SAS），
∴∠CEO=∠CDO=90°，
∴CE是⊙O的切线．
证明：连接CO，∵BC=OB，
∴∠1=∠2，
∵∠AOB=90°，
∴∠2+∠4=90°，
∵OD⊥AB，
∴∠1+∠3=90°，
∴∠3=∠4，
在△CEO和△CDO中
|
∴△CEO≌△CDO（SAS），
∴∠CEO=∠CDO=90°，
∴CE是⊙O的切线．
点评：此题主要考查了切线的判定，关键是掌握切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．
练习册系列答案
相关题目
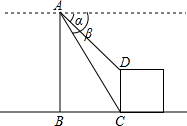关于三角函数有如下的公式：sin（α+β）=sinαcosβ+cosαsinβ；
如图，直线CD和∠AOB两边相交于点M，N，已知∠α+∠β=180°．