题目内容
6. 如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:(1)△ACE≌△BCD;
(2)$\frac{AG}{GC}$=$\frac{AF}{FE}$.
分析 (1)由三角形ABC与三角形CDE都为等边三角形,利用等边三角形的性质得到两对边相等,一对角相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)由(1)得出的三角形全等得到对应角相等,再由一对角相等,且夹边相等,利用ASA得到三角形GCD与三角形FCE全等,利用全等三角形对应边相等得到CG=CF,进而确定出三角形CFG为等边三角形,确定出一对内错角相等,进而得到GF与CE平行,利用平行线等分线段成比例即可得证.
解答 证明:(1)∵△ABC与△CDE都为等边三角形,
∴AC=BC,CE=CD,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
(2)∵△ACE≌△BCD,
∴∠BDC=∠AEC,
在△GCD和△FCE中,
$\left\{\begin{array}{l}{∠GCD=∠FCE=60°}\\{CD=CE}\\{∠BDC=∠AEC}\end{array}\right.$,
∴△GCD≌△FCE(ASA),
∴CG=CF,
∴△CFG为等边三角形,
∴∠CGF=∠ACB=60°,
∴GF∥CE,
∴$\frac{AG}{GC}$=$\frac{AF}{FE}$.
点评 此题考查了全等三角形的判定与性质,相似三角形的判定与性质,以及等边三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
16. 如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
 如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )| A. | 55° | B. | 45° | C. | 35° | D. | 65° |
1.已知关于x的不等式组$\left\{\begin{array}{l}{2x+m>0}\\{x-1<6}\end{array}\right.$有五个整数解,m的取值范围是( )
| A. | -4≤m<-2 | B. | -4<m<-2 | C. | -4<m≤-2 | D. | -4≤m≤-2 |
18. 如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
 如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )| A. | $\frac{243}{{2}^{9}}$ | B. | $\frac{81\sqrt{3}}{{2}^{9}}$ | C. | $\frac{81}{{2}^{9}}$ | D. | $\frac{81\sqrt{3}}{{2}^{8}}$ |
15. 一个几何体的三视图如图所示,则该几何体的形状可能是( )
一个几何体的三视图如图所示,则该几何体的形状可能是( )
 一个几何体的三视图如图所示,则该几何体的形状可能是( )
一个几何体的三视图如图所示,则该几何体的形状可能是( )| A. |  | B. |  | C. |  | D. |  |
16.一个不透明的盒子中装有3个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 “综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.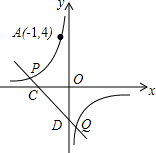 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.