题目内容
12．
如图，小红想用一条彩带缠绕易拉罐，正好从A点绕到正上方B点共四圈，已知易拉罐底面周长是12cm，高是20cm，那么所需彩带最短的是（ ）| A． | 13cm | B． | 4$\sqrt{61}$cm | C． | 4$\sqrt{34}$cm | D． | 52cm |
分析 要求彩带的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线段长时，借助于勾股定理．
解答 解：由图可知，彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处，将易拉罐表面切开展开呈长方形，则螺旋线长为四个长方形并排后的长方形的对角线长，
∵易拉罐底面周长是12cm，高是20cm，
∴x2=（12×4）2+202，
所以彩带最短是52cm．
故选D
点评 本题考查了平面展开-最短路径问题，圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决．
练习册系列答案
应用题作业本系列答案
相关题目
用小正方体搭一个几何体，使它的主视图和俯视图如图所示，这样的几何体需要小正方体最多几块？最少几块？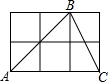
如图，六个正方形组成一个矩形，A，B，C均在格点上，则∠ABC的正切值为3．
如图，方格纸中有三个格点A、B、C，则点A到BC的距离为=$\frac{9}{5}$$\sqrt{5}$．
2．
如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若∠AOB=90°，若OA=4，则图中圆环的面积大小为（ ）
如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若∠AOB=90°，若OA=4，则图中圆环的面积大小为（ ）| A． | 2π | B． | 4π | C． | 6π | D． | 8π |