题目内容
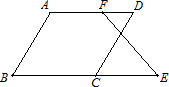
 26、在括号内填写理由.(1)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
26、在括号内填写理由.(1)如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD (
同旁内角互补,两直线平行
)∴∠B=∠DCE(
两直线平行,同位角相等
)又∵∠B=∠D(已知 ),
∴∠DCE=∠D (
等量代换
)∴AD∥BE(
内错角相等,两直线平行
)∴∠E=∠DFE(
两直线平行,内错角相等
)(2)已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB
 证明:∵DG⊥BC,AC⊥BC(
证明:∵DG⊥BC,AC⊥BC(已知
)∴∠DGB=∠ACB=90°(
垂直的定义
)∴DG∥AC(
同位角相等,两直线平行
)∴∠2=
∠DCA
(两直线平行,同位角相等
)∵∠1=∠2(
已知
)∴∠1=∠DCA(等量代换
)∴EF∥CD(
同位角相等,两直线平行
)∴∠AEF=∠ADC(
两直线平行,同位角相等
)∵EF⊥AB∴∠AEF=90° (
垂直的定义
)∴∠ADC=90° (
等量代换
)即CD⊥AB(
垂直的定义
)分析:根据平行线的性质与判定定理即可作出解决.
解答::∵∠B+∠BCD=180°(已知),
∴AB∥CD ( 同旁内角互补,两直线平行)
∴∠B=∠DCE( 两直线平行,同位角相等)
又∵∠B=∠D(已知 ),
∴∠DCE=∠D ( 等量代换)
∴AD∥BE( 内错角相等,两直线平行)
∴∠E=∠DFE( 两直线平行,内错角相等)
(2)已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB
 证明:∵DG⊥BC,AC⊥BC( 已知)
证明:∵DG⊥BC,AC⊥BC( 已知)
∴∠DGB=∠ACB=90°( 垂直的定义)
∴DG∥AC( 同位角相等,两直线平行)
∴∠2=∠DCA( 两直线平行,同位角相等)
∵∠1=∠2( 已知)∴∠1=∠DCA( 等量代换)
∴EF∥CD( 同位角相等,两直线平行)
∴∠AEF=∠ADC( 两直线平行,同位角相等)
∵EF⊥AB∴∠AEF=90° ( 垂直的定义)
∴∠ADC=90° ( 等量代换)
即CD⊥AB( 垂直的定义)
∴AB∥CD ( 同旁内角互补,两直线平行)
∴∠B=∠DCE( 两直线平行,同位角相等)
又∵∠B=∠D(已知 ),
∴∠DCE=∠D ( 等量代换)
∴AD∥BE( 内错角相等,两直线平行)
∴∠E=∠DFE( 两直线平行,内错角相等)
(2)已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:CD⊥AB
 证明:∵DG⊥BC,AC⊥BC( 已知)
证明:∵DG⊥BC,AC⊥BC( 已知)∴∠DGB=∠ACB=90°( 垂直的定义)
∴DG∥AC( 同位角相等,两直线平行)
∴∠2=∠DCA( 两直线平行,同位角相等)
∵∠1=∠2( 已知)∴∠1=∠DCA( 等量代换)
∴EF∥CD( 同位角相等,两直线平行)
∴∠AEF=∠ADC( 两直线平行,同位角相等)
∵EF⊥AB∴∠AEF=90° ( 垂直的定义)
∴∠ADC=90° ( 等量代换)
即CD⊥AB( 垂直的定义)
点评:本题考查了平行线的性质定理以及判定定理,关键性质定理与判定定理二者之间的区别以及正确掌握同位角、内错角、同旁内角的定义.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 27、在括号内填写理由.
27、在括号内填写理由.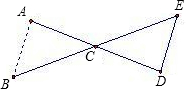 下图是小明的证明思路,请你在括号内填写理由:
下图是小明的证明思路,请你在括号内填写理由: 25、在括号内填写理由.
25、在括号内填写理由. 20、完成以下证明,并在括号内填写理由:
20、完成以下证明,并在括号内填写理由: 如图,∠1=85°,∠2=134°,∠ACD=95°.
如图,∠1=85°,∠2=134°,∠ACD=95°.