题目内容
9.先化简,再求值:$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$÷(a+$\frac{2ab+{b}^{2}}{a}$),其中a=2sin45°-1,b=tan45°.分析 先根据分式混合运算的法则把原式进行化简,再由特殊角的三角函数值计算出a的值,把a的值代入进行计算即可.
解答 解:原式=$\frac{a+b}{a}$÷$\frac{(a+b)^{2}}{a}$
=$\frac{a+b}{a}$•$\frac{a}{(a+b)^{2}}$
=$\frac{1}{a+b}$,
当a=2sin45°-1=2×$\frac{\sqrt{2}}{2}$-1=$\sqrt{2}$-1,b=tan45°=1时,
原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值及特殊角的三角函数值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.在Rt△ABC中,∠C=90°,已知a和A,有下列结论:①c=asinA;②c=$\frac{a}{sinA}$;③c=acosA;④c=$\frac{a}{cosA}$.其中,正确的结论是②.
1. 如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )
如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )
 如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )
如图是一个台阶示意图,每一层台阶的高都是20cm,宽都是50cm,长都是40cm,一只蚂蚁沿台阶从点A出发到点B,其爬行的最短线路的长度是( )| A. | 100cm | B. | 120cm | C. | 130cm | D. | 150cm |
10.已知x=-2是方程ax+4x=2的解,则a的值是( )
| A. | -5 | B. | 3 | C. | 5 | D. | -3 |
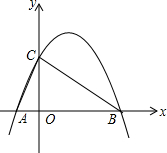 如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点(A左、右B),与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于A、B两点(A左、右B),与y轴交于点C.