题目内容
若圆的内接正六边形的半径为R,则该正六边形的内切圆的半径为( )
| A、R | ||||
B、
| ||||
C、
| ||||
D、
|
考点:正多边形和圆
专题:
分析:根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
解答:解:如图,连接OA、OB,OG;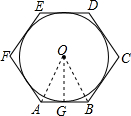
∵六边形ABCDEF是边长为R的正六边形,
∴△OAB是等边三角形,
∴OA=AB=R,
∴OG=OA•sin60°=R×
=
R.
即该正六边形的内切圆的半径为:
R.
故选D.

∵六边形ABCDEF是边长为R的正六边形,
∴△OAB是等边三角形,
∴OA=AB=R,
∴OG=OA•sin60°=R×
| ||
| 2 |
| ||
| 2 |
即该正六边形的内切圆的半径为:
| ||
| 2 |
故选D.
点评:此题考查了正多边形与圆的知识以及等边三角形的性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
若x2+x-1=0,则代数式2x2+2x-8的值为( )
| A、6 | B、8 | C、-8 | D、-6 |
线段4cm、16cm的比例中项为( )
| A、20cm | B、64cm |
| C、±8cm | D、8cm |
 如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=4,AB=5,则tan∠BCD等于( )
如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=4,AB=5,则tan∠BCD等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
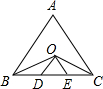 如图所示,在等边△ABC中,∠B、∠C的平分线交于点O,过O作OD∥AB、OE∥AC分别与BC交于D、E.若△ABC的周长为m,试求OD+DE+OE的长.
如图所示,在等边△ABC中,∠B、∠C的平分线交于点O,过O作OD∥AB、OE∥AC分别与BC交于D、E.若△ABC的周长为m,试求OD+DE+OE的长.