题目内容
已知,圆的两条弦AB、CD的长分别是18和24,且AB∥CD,又两弦之间的距离为3.
(1)根据题意画出符合条件的图形;
(2)求圆的半径.
(1)根据题意画出符合条件的图形;
(2)求圆的半径.
考点:垂径定理,勾股定理
专题:分类讨论
分析:(1)根据题意可分两种情况画图;
(2)如图1,作OE⊥AB于E,交CD于F,根据平行线的性质得OF⊥CD,利用垂径定理得AE=BE=
AB=9,CF=DF=
CD=12,且EF=3,设圆的半径为r,OF=x,则OE=3-x,根据勾股定理得122+x2=r2,92+(3-x)2=r2,接着消去r得到122+x2=92+(3-x)2,解得x=-9(舍去);如图2,同样可得AE=BE=
AB=9,CF=DF=
CD=12,EF=3,设圆的半径为r,OF=x,则OE=3+x,利用勾股定理得92+(3+x)2=r2,122+x2=92+(3+x)2,消去r可解得x=9,最后利用勾股可计算出r=15.
(2)如图1,作OE⊥AB于E,交CD于F,根据平行线的性质得OF⊥CD,利用垂径定理得AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)如图;
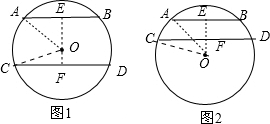
(2)如图1,作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=
AB=9,CF=DF=
CD=12,EF=3,
设圆的半径为r,OF=x,则OE=3-x,
在Rt△OCF中,122+x2=r2,
在Rt△AEO中,92+(3-x)2=r2,
∴122+x2=92+(3-x)2,解得x=-9(舍去);
如图2,作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=
AB=9,CF=DF=
CD=12,EF=3,
设圆的半径为r,OF=x,则OE=3+x,
在Rt△OCF中,122+x2=r2,
在Rt△AEO中,92+(3+x)2=r2,
∴122+x2=92+(3+x)2,解得x=9,
∴r=
=15.
∴圆的半径为15.

(2)如图1,作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
设圆的半径为r,OF=x,则OE=3-x,
在Rt△OCF中,122+x2=r2,
在Rt△AEO中,92+(3-x)2=r2,
∴122+x2=92+(3-x)2,解得x=-9(舍去);
如图2,作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
设圆的半径为r,OF=x,则OE=3+x,
在Rt△OCF中,122+x2=r2,
在Rt△AEO中,92+(3+x)2=r2,
∴122+x2=92+(3+x)2,解得x=9,
∴r=
| 122+92 |
∴圆的半径为15.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
若圆的内接正六边形的半径为R,则该正六边形的内切圆的半径为( )
| A、R | ||||
B、
| ||||
C、
| ||||
D、
|
将一直角三角形的三边长变为原来的2.5倍后,得到的三角形是( )
| A、锐角三角形 | B、钝角三角形 |
| C、直角三角形 | D、无法确定 |
下列哪个是分式方程( )
A、-
| ||
B、
| ||
C、
| ||
| D、2x2+3x=-2 |
 如图,在Rt△ABC和Rt△BAD中,CE=DE,∠C=∠D=90°.
如图,在Rt△ABC和Rt△BAD中,CE=DE,∠C=∠D=90°.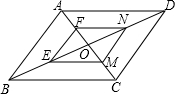 如图,在?ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点,这样形成一个?FEMN,你能证明?ABCD∽?FEMN吗?
如图,在?ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO的中点,这样形成一个?FEMN,你能证明?ABCD∽?FEMN吗?