题目内容
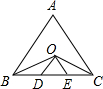 如图所示,在等边△ABC中,∠B、∠C的平分线交于点O,过O作OD∥AB、OE∥AC分别与BC交于D、E.若△ABC的周长为m,试求OD+DE+OE的长.
如图所示,在等边△ABC中,∠B、∠C的平分线交于点O,过O作OD∥AB、OE∥AC分别与BC交于D、E.若△ABC的周长为m,试求OD+DE+OE的长.考点:等边三角形的判定与性质
专题:
分析:由条件可证明∠OBD=∠BOD,可得OD=BD,同理可得OE=EC,所以OD+DE+OE=BC,再利用△ABC的周长求出BC的长即可.
解答:解:∵OD∥AB,BO平分∠ABC,
∴∠ABO=∠BOD=∠OBD,
∴OD=BD,
同理可得OE=EC,
∴OD+DE+OE=BD+DE+EC=BC,
∵△ABC为等边三角形,且周长为m,
∴BC=
,
∴OD+DE+OE=
.
∴∠ABO=∠BOD=∠OBD,
∴OD=BD,
同理可得OE=EC,
∴OD+DE+OE=BD+DE+EC=BC,
∵△ABC为等边三角形,且周长为m,
∴BC=
| m |
| 3 |
∴OD+DE+OE=
| m |
| 3 |
点评:本题主要考查等边三角形的性质及平行线的性质、角平分线的定义,由条件求得OD=BD、OE=EC,把所求问题转化成求△ABC的边长是解题的关键.

练习册系列答案
相关题目
若圆的内接正六边形的半径为R,则该正六边形的内切圆的半径为( )
| A、R | ||||
B、
| ||||
C、
| ||||
D、
|
将一直角三角形的三边长变为原来的2.5倍后,得到的三角形是( )
| A、锐角三角形 | B、钝角三角形 |
| C、直角三角形 | D、无法确定 |
下列哪个是分式方程( )
A、-
| ||
B、
| ||
C、
| ||
| D、2x2+3x=-2 |
若
的值在两个整数a与a+1之间,则a的值为( )
| 17 |
| A、3 | B、4 | C、5 | D、6 |
下列计算错误的是( )
A、
| ||||||
B、3
| ||||||
C、
| ||||||
D、当x<1时,
|
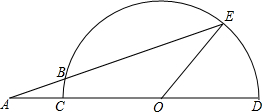 如图,已知CD是半圆的直径,O是圆心,E是半圆上一点,且∠EOD=45°,A是DC延长线上的一点,AE交半圆于点B,AB=OC=2,求弓形BE的高.
如图,已知CD是半圆的直径,O是圆心,E是半圆上一点,且∠EOD=45°,A是DC延长线上的一点,AE交半圆于点B,AB=OC=2,求弓形BE的高.